��Ŀ����
����Ŀ��ij��װ������һ��������ÿ������![]() Ԫ����ʼ��ÿ��
Ԫ����ʼ��ÿ��![]() Ԫ�ļ۸����ۣ�ÿ����������
Ԫ�ļ۸����ۣ�ÿ����������![]() �������������ѹ�������������ۣ������ν��ۺ��ÿ���ۼ�
�������������ѹ�������������ۣ������ν��ۺ��ÿ���ۼ�![]() Ԫ��ÿ����������
Ԫ��ÿ����������![]() ����
����
![]() ��֪���ν��۰ٷ�����ͬ����ÿ�ν��۵İٷ��ʣ�
��֪���ν��۰ٷ�����ͬ����ÿ�ν��۵İٷ��ʣ�
![]() �����ĵ����ڽ��۹����з��֣��ʵ��Ľ��ۼȿ����������ֿ��������룬��ÿ�������ۼ�ÿ����
�����ĵ����ڽ��۹����з��֣��ʵ��Ľ��ۼȿ����������ֿ��������룬��ÿ�������ۼ�ÿ����![]() Ԫ�����ۻ�����
Ԫ�����ۻ�����![]() ������������Ҫÿ���ڻ���
������������Ҫÿ���ڻ���![]() Ԫ��Ӧ���ۼ۶�Ϊ����Ԫ��
Ԫ��Ӧ���ۼ۶�Ϊ����Ԫ��
���𰸡�Ӧ���ۼ۶�Ϊ185Ԫ��175Ԫ��
��������
��1��������������г���Ӧ�ķ��̣��Ӷ��������ÿ�ν��۵İٷ��ʣ�
��2��������������г���Ӧ�ķ��̣������Ӧ���ۼ�.
�⣺![]() ��ÿ�ν��۵İٷ���Ϊ
��ÿ�ν��۵İٷ���Ϊ![]() ��
��
![]()
��ã�![]() ��
��![]() ����ȥ����
����ȥ����
��ÿ�ν��۵İٷ�����![]() ��
��
![]() ��������ۼ۽���
��������ۼ۽���![]() Ԫ��
Ԫ��
![]()
��ã�![]() ��
��![]()
��![]() ��
��![]() ��
��
��Ӧ���ۼ۶�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ.
Ԫ.

 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д� ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�����Ŀ��ij���Ϊ��ӭ������������ƶ��˻�ƻ��������ǻ�ƻ���IJ�����Ϣ��
�����������ƻ��� | ||
�鱾��� | A�� | B�� |
����(��λ��Ԫ) | 18 | 12 |
��ע | 1.�ò�����16800Ԫ����A��B����ͼ�鹲1000���� 2��A��ͼ�鲻����600���� ���� |
(1)�¾����鿴�ƻ���ʱ���֣�A��ͼ��ı����B��ͼ���۵�1.5�������˿���540Ԫ����ͼ�飬�ܵ�������A��ͼ�������ǡ�ñȵ�������B��ͼ���������10���������A��B����ͼ��ı�ۣ�
(2)���г�����¾����������Ǹ߹��������������ͼ�����۵�Ӱ�죬����������۷�����A��ͼ��ÿ����۽���aԪ(0��a��5)���ۣ�B��ͼ��۸䣬��ô���Ӧ��ν������ܻ���������
����Ŀ��Ϊ�������ǽ�Լ��ˮ����ʱ��©ˮ��ˮ��ͷ��С��ͬѧ����ˮ��ͷ©ˮʵ�飬ÿ��10��۲���Ͳ��ˮ���������¼�����������©����ˮ����ȷ��1����������֪���ڽ�ˮ����Ͳ�������Ϊ100������
ʱ��t���룩 | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
��Ͳ��ˮ��v�������� | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
��1����ͼ�е�ƽ��ֱ������ϵ�У��ԣ�t,v��Ϊ��������ϱ������ݶ�Ӧ�ĵ㣻
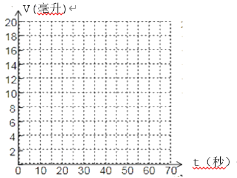
��2���ù⻬���������Ӹ��㣬��²�V��t�ĺ�����ϵʽ��______________��
��3��������⣺
��С��ͬѧ������Ͳ��ʼʵ��ǰԭ�д�ˮ ������
�����С��ͬѧ����ʵ�飬����Ͳ�е�ˮ�պ�ʢ��ʱ������ʱ����_____����
������©ˮ�ٶȣ���Сʱ��©ˮ ������
����Ŀ��ijУҪ������ѧ�����������س������¡��ź�����ѡһ�˲μ�У����Զ����������Զר������Լ��Ժ��![]() ����Զѡ�����У����ǵijɼ�����λ��
����Զѡ�����У����ǵijɼ�����λ��![]() �����±���ʾ��
�����±���ʾ��
ר����Ժ� | ƽ���� | ���� | |||||||
���� |
|
|
|
|
|
|
|
| |
�ź� |
|
|
|
|
|
|
|
| |
![]() ���ź�ͬѧ
���ź�ͬѧ![]() �β��Գɼ���ƽ����������ͬѧ
�β��Գɼ���ƽ����������ͬѧ![]() �β��Գɼ��ķ��
�β��Գɼ��ķ��
![]() ����ֱ��ƽ�����ͷ���ĽǶȷ������˳ɼ����ص㣻
����ֱ��ƽ�����ͷ���ĽǶȷ������˳ɼ����ص㣻
![]() ������������������ϣ��ɼ����ﵽ
������������������ϣ��ɼ����ﵽ![]() ���ͺܿ��ܵõ��ھ�������ΪӦѡ˭ȥ������ھ��Ƚ��а��գ�˵�����ɣ�
���ͺܿ��ܵõ��ھ�������ΪӦѡ˭ȥ������ھ��Ƚ��а��գ�˵�����ɣ�
![]() �����ĸ�����óɼ��ļ�¼��
�����ĸ�����óɼ��ļ�¼��![]() ����Ҫ����Ƽ�¼������ΪӦѡ˭ȥ������
����Ҫ����Ƽ�¼������ΪӦѡ˭ȥ������