Question

【题目】如图，以的直角边为直径的半圆与斜边交于点，是边的中点，连接．

求证：是半圆的切线；

若、的长是方程的个根，求直角边的长．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

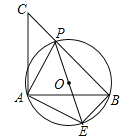
（1）连OD，OE，由E是BC边上的中点，得到OE是△ABC的中位线，则OE∥AC，所以有∠1=∠3，∠2=∠A，而∠A=∠3，因此得到∠1=∠2，再证明△OED≌△OEB，于是∠OED=∠OBE=90°；

（2）首先解方程x2﹣10x+24=0，从而求出AD、AB的长，再证明△ABC∽△ADB，得出，即可求出答案．

（1）连OD，OE，如图，∵E是BC边上的中点，AB是半圆O的直径，∴OE是△ABC的中位线，∴OE∥AC，∴∠1=∠3，∠2=∠A．

∵OD=OA，∴∠A=∠3，∴∠1=∠2．

又∵OD=OB，OE=OE，∴△OED≌△OEB，∴∠ODE=∠OBE=90°，∴DE与半圆O相切．

（2）连接BD．

∵AD、AB的长是方程x2﹣10x+24=0的个根，AB为圆的直径，∴AD=4，AB=6．

∵AB为直径，∴∠ADB=∠ABC=90°．

∵∠CAB=∠CAB，∴△ABC∽△ADB，∴，∴，∴AC=9，∴BC=3．