题目内容
设函数f（x）=
，则f（
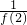）的值为
- A.
- B.-
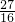
- C.
- D.18
A
分析：当x＞1时，f（x）=x2+x-2； 当x≤1时，f（x）=1-x2，故此本题先求=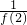
．再将所求得的值代入x＞1时解析式求值．
解答：当x＞1时，f（x）=x2+x-2，则 f（2）=22+2-2=4，
∴
，
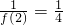当x≤1时，f（x）=1-x2，
∴f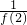（）=f（）=1-
=．
故选A．
点评：本题考查分段复合函数求值，根据定义域选择合适的解析式，由内而外逐层求解．属于考察分段函数的定义的题型．
分析：当x＞1时，f（x）=x2+x-2； 当x≤1时，f（x）=1-x2，故此本题先求
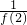=．再将所求得的值代入x＞1时解析式求值．解答：当x＞1时，f（x）=x2+x-2，则 f（2）=22+2-2=4，
∴
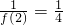，当x≤1时，f（x）=1-x2，
∴f（
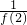）=f（）=1-=．故选A．
点评：本题考查分段复合函数求值，根据定义域选择合适的解析式，由内而外逐层求解．属于考察分段函数的定义的题型．
练习册系列答案
相关题目
设函数y=kx（k＞0）与
工业园区消费群体相对固定．
某市自来水公司对居民用水采用以户为单位分段计费办法收费．即一个月用水10吨以内（包括10吨）用户，每吨收水费a元；一个月用水超过10吨的用户，10吨水仍按每吨a元收费，超过的部分每吨按b元（b＞a）收费．设一户居民月用水缴费y元，用水量x吨，y与x之间的函数关系如图所示，则b的值为（ ）