题目内容
 如图,AB=DE,AC=DF,BE=CF.求证:AC∥DF.
如图,AB=DE,AC=DF,BE=CF.求证:AC∥DF.
分析:要证AC∥DF的关键是正∠B=∠DEF,也就是正三角形ABC和DEF全等,已知了这两个三角形三组对应边相等,由此可得出三角形全等.
解答:证明:∵BE=CF,BE+CE=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
.
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE(全等三角形的对应角相等),
∴AC∥DF(同位角相等,两直线平行).
∴BC=EF,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SSS),
∴∠ACB=∠DFE(全等三角形的对应角相等),
∴AC∥DF(同位角相等,两直线平行).
点评:本题考查了全等三角形的判定和性质及平行线的判断等知识;根据全等三角形来得出对应的角相等,是解此类题的常用方法.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,AB∥DE,BC∥EF,则①
如图,AB∥DE,BC∥EF,则①| OA |
| OD |
| OB |
| OE |
| OC |
| OF |
| OB |
| OE |
| A、① | B、② | C、①② | D、①②③ |
 7、如图,AB∥DE,∠E=65°,则∠B+∠C=( )
7、如图,AB∥DE,∠E=65°,则∠B+∠C=( )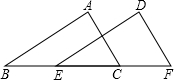 已知:如图,AB∥DE,且AB=DE.
已知:如图,AB∥DE,且AB=DE. 9、如图,AB∥DE,∠E=65°,则∠B+∠C=
9、如图,AB∥DE,∠E=65°,则∠B+∠C= 已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?
已知:如图,AB=DE,CD=FA,∠A=∠D,∠AFC=∠DCF,则BC=EF.你能说出它们相等的理由吗?