题目内容
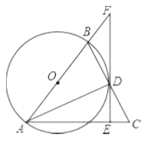
【题目】对于直角坐标系 xOy 中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,使得点P在射线BC上,且∠APB=![]() ∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
∠ACB(0°<∠ACB<180°),则称P为⊙C的依附点.
(1)当⊙O的半径为1时
①已知点D(﹣1,0),E(0,﹣2),F(2.5,0),在点D,E,F中,⊙O的依附点是___;
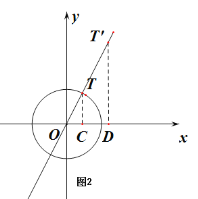
②点T在直线y=![]() x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
x上,若T为⊙O的依附点,求点T的横坐标t的取值范围;
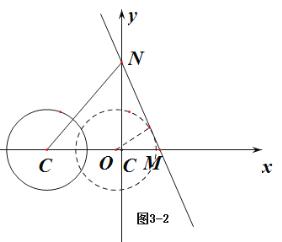
(2)⊙C的圆心在x轴上,半径为1,直线 y=﹣2x+2与x轴、y 轴分别交于点M、N,若线段MN上的所有点都是⊙C 的依附点,请求出圆心C的横坐标n的取值范围.
【答案】(1)①![]() 、
、![]() ;②
;②![]() 或
或![]() ;
;
(2)![]() 或
或![]() .
.
【解析】
(1)①如图1中,根据![]() 为
为![]() 的依附点,可知:当
的依附点,可知:当![]() 为
为![]() 的半径)时,点
的半径)时,点![]() 为
为![]() 的依附点,由此即可判断.
的依附点,由此即可判断.
②分两种情形:点![]() 在第一象限或点
在第一象限或点![]() 在第三象限分别求解即可.
在第三象限分别求解即可.
(2)分两种情形:点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 在点
在点![]() 的左侧分别求解即可解决问题.
的左侧分别求解即可解决问题.
解:(1)①如图1中,根据![]() 为
为![]() 的依附点,可知:当
的依附点,可知:当![]() 为
为![]() 的半径)时,点
的半径)时,点![]() 为
为![]() 的依附点.
的依附点.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() 是
是![]() 的依附点,
的依附点,
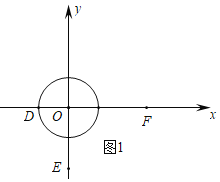
故答案为:![]() 、
、![]() ;
;
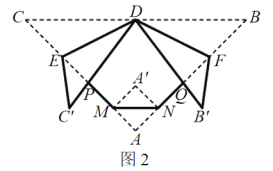
(2)如图2,
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() 点
点![]() 在第一象限或第三象限,直线
在第一象限或第三象限,直线![]() 与
与![]() 轴所夹的锐角为
轴所夹的锐角为![]() ,
,
当点![]() 在第一象限,当
在第一象限,当![]() 时,作
时,作![]() 轴垂足为C,易求点
轴垂足为C,易求点![]() ,
,![]() ;
;
当![]() 时,作
时,作![]() 轴,易求
轴,易求![]() ,
,![]() ,
,
![]() 满足条件的点
满足条件的点![]() 的横坐标
的横坐标![]() 的取值范围
的取值范围![]() ,
,
当点![]() 在第三象限,同理可得满足条件的点
在第三象限,同理可得满足条件的点![]() 的横坐标
的横坐标![]() 的取值范围
的取值范围![]() ,
,
综上所述:满足条件的点![]() 的横坐标
的横坐标![]() 的取值范围:
的取值范围:![]() 或
或![]() ,
,
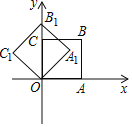
(3)![]() 由题意直线 y=﹣2x+2与x轴、y 轴分别交点坐标为:
由题意直线 y=﹣2x+2与x轴、y 轴分别交点坐标为:![]() ,
,![]() .
.
如图![]() 中,当点
中,当点![]() 在点
在点![]() 的右侧时,
的右侧时,
当![]() 时,
时,![]() ,此时
,此时![]() ,
,![]() ;
;
当![]() 时,此时
时,此时![]() .
.
![]() 满足条件的
满足条件的![]() 的值的范围为
的值的范围为![]() .
.
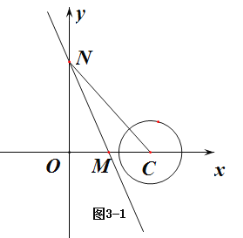
如图![]() 中,当点
中,当点![]() 在点
在点![]() 的右侧时,
的右侧时,
当![]() 与直线
与直线![]() 相切时,易知
相切时,易知![]() ;
;
当![]() 时,
时,![]() .
.
![]() 满足条件的n的值的范围为
满足条件的n的值的范围为![]() .
.
综上所述,满足条件的![]() 的值的范围为:
的值的范围为:![]() 或
或![]() .
.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目