题目内容
【题目】用一张斜边![]() 长为
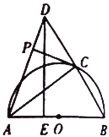
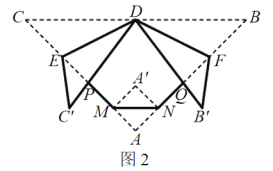
长为![]() 的等腰直角三角形纸片进行折“狗脸”活动(如图1所示) .第一步,如图2,沿
的等腰直角三角形纸片进行折“狗脸”活动(如图1所示) .第一步,如图2,沿![]() 向后折一个面积为1的等腰直角三角形
向后折一个面积为1的等腰直角三角形![]() ;第二步,在直角边
;第二步,在直角边![]() .上各取一点
.上各取一点![]() 为
为![]() 的中点,将
的中点,将![]() 分别沿
分别沿![]() 折叠,使得点
折叠,使得点![]() 对应点
对应点![]() 落在直线
落在直线![]() 上,
上,![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,则“狗脸”(图形
,则“狗脸”(图形![]() )的面积为__________.
)的面积为__________.
【答案】![]()
【解析】
根据题意添加适当的辅助线构造出直角三角形,利用等腰三角形的性质、翻折的性质即可求得答案.
解:连接![]() 、
、![]() 、
、![]() 分别于点
分别于点![]() 、
、![]() 的连线交于点
的连线交于点![]() 、
、![]() 、
、![]() ,如图:
,如图:

根据已知条件和翻折的性质可知![]()
∵![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
∵![]() 是面积为
是面积为![]() 的等腰直角三角形,将
的等腰直角三角形,将![]() 沿
沿![]() 向后折到
向后折到![]() 的位置
的位置
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴设![]() ,
,![]()
∴![]() 都是等腰直角三角形
都是等腰直角三角形
∴![]()
∴![]()
∴![]()
∴![]()
∵由翻折的性质可得![]() ,由平行线的性质可得
,由平行线的性质可得![]()
∴![]()
∴![]()
∴设![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴![]()
![]()
![]() .
.
故答案是:![]()

练习册系列答案
相关题目