题目内容
通过配方，确定抛物线y=-2x2-5x+7的开口方向、对称轴和顶点坐标．
解：y=-2x2-5x+7
=-2（x2+
x）+7
=-2（x+
）2+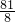
，
∵a=-2＜0，
∴抛物线开口向下，
对称轴是直线x=-，
顶点坐标为（-，）．
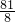分析：先运用配方法：提出二次项系数，加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式，即y=a（x-h）2+k的形式，再根据二次函数的性质，即可求出开口方向、对称轴和顶点坐标．
点评：本题考查了二次函数的性质，重点是掌握开口方向的判定、对称轴及顶点坐标的求法．
=-2（x2+
x）+7=-2（x+
）2+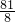，∵a=-2＜0，
∴抛物线开口向下，
对称轴是直线x=-
，顶点坐标为（-
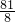，）．分析：先运用配方法：提出二次项系数，加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式，即y=a（x-h）2+k的形式，再根据二次函数的性质，即可求出开口方向、对称轴和顶点坐标．
点评：本题考查了二次函数的性质，重点是掌握开口方向的判定、对称轴及顶点坐标的求法．
练习册系列答案
相关题目