题目内容
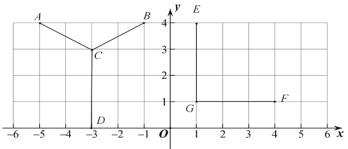
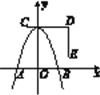
【题目】如图是8×8的标准点阵图，直线l、m互相垂直，已知△ABC.
（1）写出△ABC的形状；
（2）分别画出△ABC关于直线l、m对称的△A1B1C1，△A2B2C2，再画出△A1B1C1关于直线m对称的△A3B3C3
（3）△A2B2C2与△A3B3C3关于哪条直线对称？ （填“直线l、m”）
【答案】（1）△ABC是等腰直角三角形；（2）见解析；（3）l.
【解析】
（1）由勾股定理求出三边长，再运用勾股定理的逆定理可判断出△ABC的形状；
（2）利用关于直线对称点的性质得出对应点连接得出图形；
（3）观察图形可得出结果。
解：（1）△ABC是等腰直角三角形.
理由：把相邻两格式的距离看作1，由勾股定理可得：
∴△ABC是等腰直角三角形.
（2）如图所示，
(3)由图可得：
△A2B2C2与△A3B3C3关于直线l对称.
故答案为：l.
练习册系列答案
相关题目
