ĖâÄŋÄÚČÝ
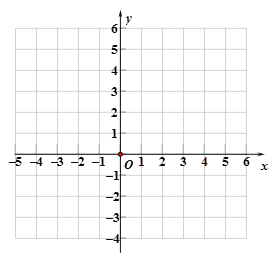
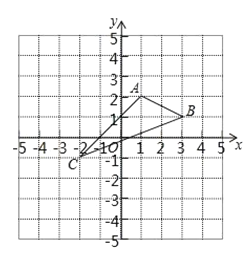
ĄūĖâÄŋĄŋČįÍžĢŽķĨĩãΊCĩÄÅŨÎïÏßy=ax2+bxĢĻaĢū0ĢĐūđýĩãAšÍxÖáÕý°ëÖáÉÏĩÄĩãBĢŽÁŽ―ÓOCĄĒOAĄĒABĢŽŌŅÖŠOA=OB=2ĢŽĄÏAOB=120ĄãĢŪ
ĢĻ1ĢĐĮóÕâĖõÅŨÎïÏßĩÄąíīïĘ―Ģŧ
ĢĻ2ĢĐđýĩãCŨũCEĄÍOBĢŽīđŨãΊEĢŽĩãPΊyÖáÉÏĩÄķŊĩãĢŽČôŌÔOĄĒCĄĒPΊķĨĩãĩÄČý―ĮÐÎÓëĄũAOEÏāËÆĢŽĮóĩãPĩÄŨøąęĢŧ
ĢĻ3ĢĐČô―ŦĢĻ2ĢĐĩÄÏßķÎOEČÆĩãOÄæĘąÕëÐýŨŠĩÃĩ―OEĄäĢŽÐýŨŠ―ĮΊĶÁĢĻ0ĄãĢžĶÁĢž120ĄãĢĐĢŽÁŽ―ÓEĄäAĄĒEĄäBĢŽĮóEĄäA+![]() EĄäBĩÄŨîÐĄÖĩĢŪ
EĄäBĩÄŨîÐĄÖĩĢŪ
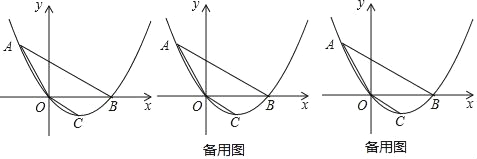
Ąūīð°ļĄŋ(1) y=![]() x2Đ
x2Đ![]() xĢŧĢĻ2ĢĐĩãPŨøąęΊĢĻ0ĢŽ
xĢŧĢĻ2ĢĐĩãPŨøąęΊĢĻ0ĢŽ![]() ĢĐŧōĢĻ0ĢŽ
ĢĐŧōĢĻ0ĢŽ![]() ĢĐĢŧĢĻ3ĢĐ
ĢĐĢŧĢĻ3ĢĐ![]() .
.
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝAO=OB=2ĢŽĄÏAOB=120ĄãĢŽĮóģöAĩãŨøąęĢŽŌÔž°BĩãŨøąęĢŽ―øķøĀûÓÃīýķĻÏĩĘý·ĻĮóķþīΚŊĘý―âÎöĘ―Ģŧ
ĢĻ2ĢĐĄÏEOC=30ĄãĢŽÓÉOA=2OEĢŽOC=![]() ĢŽÍÆģöĩąOP=
ĢŽÍÆģöĩąOP=![]() OCŧōOPĄä=2OCĘąĢŽĄũPOCÓëĄũAOEÏāËÆĢŧ
OCŧōOPĄä=2OCĘąĢŽĄũPOCÓëĄũAOEÏāËÆĢŧ
ĢĻ3ĢĐČįÍžĢŽČĄQĢĻ![]() ĢŽ0ĢĐĢŪÁŽ―ÓAQĢŽQEĄäĢŪÓÉĄũOEĄäQĄŨĄũOBEĄäĢŽÍÆģö
ĢŽ0ĢĐĢŪÁŽ―ÓAQĢŽQEĄäĢŪÓÉĄũOEĄäQĄŨĄũOBEĄäĢŽÍÆģö![]() ĢŽÍÆģöEĄäQ=
ĢŽÍÆģöEĄäQ=![]() BEĄäĢŽÍÆģöAEĄä+
BEĄäĢŽÍÆģöAEĄä+![]() BEĄä=AEĄä+QEĄäĢŽÓÉAEĄä+EĄäQĄÝAQĢŽÍÆģöEĄäA+
BEĄä=AEĄä+QEĄäĢŽÓÉAEĄä+EĄäQĄÝAQĢŽÍÆģöEĄäA+![]() EĄäBĩÄŨîÐĄÖĩūÍĘĮÏßķÎAQĩÄģĪ.
EĄäBĩÄŨîÐĄÖĩūÍĘĮÏßķÎAQĩÄģĪ.
ĢĻ1ĢĐđýĩãAŨũAHĄÍxÖáÓÚĩãHĢŽ
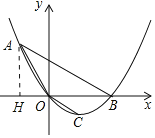
ĄßAO=OB=2ĢŽĄÏAOB=120ĄãĢŽ
ĄāĄÏAOH=60ĄãĢŽ
ĄāOH=1ĢŽAH=![]() ĢŽ
ĢŽ
ĄāAĩãŨøąęΊĢšĢĻ-1ĢŽ![]() ĢĐĢŽBĩãŨøąęΊĢšĢĻ2ĢŽ0ĢĐĢŽ
ĢĐĢŽBĩãŨøąęΊĢšĢĻ2ĢŽ0ĢĐĢŽ
―ŦÁ―ĩãīúČëy=ax2+bxĩÃĢš
![]() ĢŽ
ĢŽ
―âĩÃĢš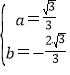 ĢŽ
ĢŽ
ĄāÅŨÎïÏßĩÄąíīïĘ―ÎŠĢšy=![]() x2-
x2-![]() xĢŧ
xĢŧ
ĢĻ2ĢĐČįÍžĢŽ
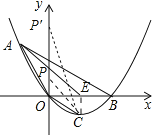
ĄßCĢĻ1ĢŽ-![]() ĢĐĢŽ
ĢĐĢŽ
ĄātanĄÏEOC=![]() ĢŽ
ĢŽ
ĄāĄÏEOC=30ĄãĢŽ
ĄāĄÏPOC=90Ąã+30Ąã=120ĄãĢŽ
ĄßĄÏAOE=120ĄãĢŽ
ĄāĄÏAOE=ĄÏPOC=120ĄãĢŽ
ĄßOA=2OEĢŽOC=![]() ĢŽ
ĢŽ
ĄāĩąOP=![]() OCŧōOPĄä=2OCĘąĢŽĄũPOCÓëĄũAOEÏāËÆĢŽ
OCŧōOPĄä=2OCĘąĢŽĄũPOCÓëĄũAOEÏāËÆĢŽ
ĄāOP=![]() ĢŽOPĄä=
ĢŽOPĄä=![]() ĢŽ
ĢŽ
ĄāĩãPŨøąęΊĢĻ0ĢŽ![]() ĢĐŧōĢĻ0ĢŽ
ĢĐŧōĢĻ0ĢŽ![]() ĢĐĢŪ
ĢĐĢŪ
ĢĻ3ĢĐČįÍžĢŽČĄQĢĻ![]() ĢŽ0ĢĐĢŪÁŽ―ÓAQĢŽQEĄäĢŪ
ĢŽ0ĢĐĢŪÁŽ―ÓAQĢŽQEĄäĢŪ
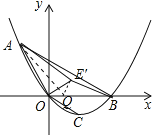
Ąß![]()
ĢŽĄÏQOEĄä=ĄÏBOEĄäĢŽ
ĄāĄũOEĄäQĄŨĄũOBEĄäĢŽ
Ąā![]() ĢŽ
ĢŽ
ĄāEĄäQ=![]() BEĄäĢŽ
BEĄäĢŽ
ĄāAEĄä+![]() BEĄä=AEĄä+QEĄäĢŽ
BEĄä=AEĄä+QEĄäĢŽ
ĄßAEĄä+EĄäQĄÝAQĢŽ
ĄāEĄäA+![]() EĄäBĩÄŨîÐĄÖĩūÍĘĮÏßķÎAQĩÄģĪĢŽŨîÐĄÖĩΊ
EĄäBĩÄŨîÐĄÖĩūÍĘĮÏßķÎAQĩÄģĪĢŽŨîÐĄÖĩΊ![]() ĢŪ
ĢŪ