Question

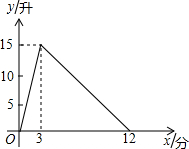（2013•厦门）一个有进水管与出水管的容器，从某时刻开始的3分内只进水不出水，在随后的9分内既进水又出水，每分的进水量和出水量都是常数．容器内的水量y（单位：升）与时间x（单位：分）之间的关系如图所示．当容器内的水量大于5升时，求时间x的取值范围．

Answer 1

分析：分别求出0≤x＜3和3≤x≤12时的函数解析式，再求出y=5时的x的值，然后根据函数图象写出x的取值范围即可．

解答：解：①0≤x＜3时，设y=mx，
则3m=15，
解得m=5，
所以，y=5x，
②3≤x≤12时，设y=kx+b，
∵函数图象经过点（3，15），（12，0），
∴

3k+b=15 12k+b=0

，
解得

k=- 5 3 b=20

，
所以，y=-

5

3

x+20，
当y=5时，由5x=5得，x=1，
由-

5

3

x+20=5得，x=9，
所以，当容器内的水量大于5升时，时间x的取值范围是1＜x＜9．

点评：本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式，以及已知函数值求自变量的方法．