题目内容
(2013•厦门)有一个质地均匀的正12面体,12个面上分别写有1~12这12个整数(每个面只有一个整数且互不相同).投掷这个正12面体一次,记事件A为“向上一面的数字是2或3的整数倍”,记事件B为“向上一面的数字是3的整数倍”,请你判断等式P(A)=
+P(B)是否成立,并说明理由.
| 1 | 2 |
分析:让向上一面的数字是2的倍数或3的倍数的情况数除以总情况数即为事件A所求的概率,进而得出事件B的概率,进而得出答案.
解答:解:不成立;
理由:
∵投掷这个正12面体一次,记事件A为“向上一面的数字是2或3的整数倍”,
∴符合要求的数有:2,3,4,6,8,9,10,12一共有8个,
则P(A)=
,
∵事件B为“向上一面的数字是3的整数倍”,
∴符合要求的数有:3,6,9,12一共有4个,
则P(B)=
,
∵
+
=
≠
,
∴P(A)≠
+P(B).
理由:
∵投掷这个正12面体一次,记事件A为“向上一面的数字是2或3的整数倍”,
∴符合要求的数有:2,3,4,6,8,9,10,12一共有8个,
则P(A)=
| 2 |
| 3 |
∵事件B为“向上一面的数字是3的整数倍”,
∴符合要求的数有:3,6,9,12一共有4个,
则P(B)=
| 1 |
| 3 |
∵
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 2 |
| 3 |
∴P(A)≠
| 1 |
| 2 |
点评:此题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
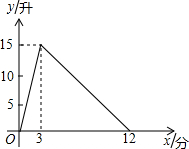 (2013•厦门)一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,求时间x的取值范围.
(2013•厦门)一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数.容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,求时间x的取值范围.