题目内容
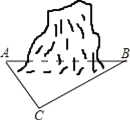
【题目】如图,在△ABC中,AB=8, AC=10,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G,连接GD,若∠EFC=60°,则EG的长为( )

A. 4B. 5C. 6D. 7
【答案】B
【解析】
连接BD取BD中点为H,连接HF、HE,利用中位线的性质及等腰三角形的性质,在△AFG中找到各角之间的关系,继而可得△AGF是等边三角形,推出GF、FE各自的边长,继而得到GE的长度.
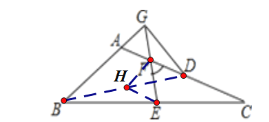
连接BD取BD中点H,连接HF、HE.
因为F是AD的中点,
所以HF∥AB,HF=![]() AB,
AB,
所以∠AGF=∠HFE,HF=4.
同理HE∥CD,HE=![]() CD,
CD,
所以∠HEF=∠EFC=60°.
又因为AB=CD=8,
所以HE=4.
因为∠HFE=60°,HE=HF=4,
所以△HEF为等边三角形,
所以EF=4.
因为∠AGE=∠AFG=60°,
所以△AGF为等边三角形.
因为F为AD中点且AD=2,
所以GF=1.
因为GE=EF+GF,
所以GE=5.

练习册系列答案
相关题目