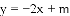题目内容
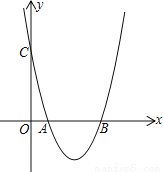
如图1，抛物线y＝x2＋bx＋c与x轴交于A(1，0)、B(4，0)，与y轴交于点C
(1) 求抛物线的解析式
(2) 抛物线上一点D，满足S△DAC＝S△OAC，求点D的坐标
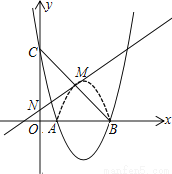
(3) 如图2，已知N(0，1)，将抛物线在点A、B之间部分（含点A、B）沿x轴向上翻折，得到图T（虚线部分），点M为图象T的顶点．现将图象保持其顶点在直线MN上平移，得到的图象T1与线段BC至少有一个交点，求图象T1的顶点横坐标的取值范围
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
有A、B两个班级,每个班级各有45名学生参加一次测验.每名参加者可获得0,1,2,3,4,5,6,7,8,9这几种不同的分值中的一种.测试结果A班的成绩如下表所示,B班的成绩如图所示.
分数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数 | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |
A班
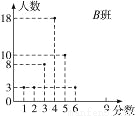
(1)由观察所得,_________________班的方差大;
(2)若两班合计共有60人及格,问参加者最少获____________分才可以及格.
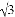≈1.732）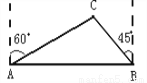
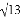，则a＝_____，b＝_____．
