Question

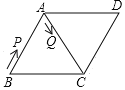
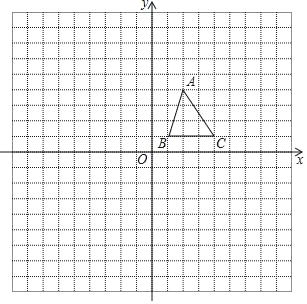
【题目】已知四边形ABCD是矩形，AB＝2，BC＝4，E为BC边上一动点且不与B、C重合，连接AE；

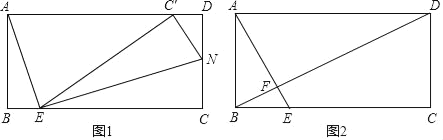
（1）如图1，过点E作EN⊥AE交CD于点N

①若BE＝1，求CN的长；②将△ECN沿EN翻折，点C恰好落在边AD上，求BE的长；

（2）如图2，连接BD，设BE＝m，试用含m的代数式表示S四边形CDFE：S△ADF值．

Answer 1

【答案】（1）①CN＝；②BE＝2或BE＝；（2）S四边形CDFE：S△ADF=1+﹣．

【解析】

（1）①求出CE=BC-BE=3，证明△ABE∽△ECF，得出＝，即可得出结果；

②过点E作EF⊥AD于F，则四边形ABEF是矩形，得出AB=EF=2，AF=BE，由折叠的性质得出CE=C′E，CN=C′N，∠EC′N=∠C=90°，证明△EC′F∽△NC′D，得出＝＝，则＝＝，由＝，得出＝，则＝＝，得出C′D=BE，设BE=x，则C′D=AF=x，C′F=4-2x，CE=4-x，则＝，＝，，求出DN=x（2-x），CN=，由CN+DN=CD=2，即可得出结果；

（2）易证△ADF∽△EBF，得出＝＝，则=（）2=，推出S△ADF=s△BEF，由同高底边比例得出S△ABF==S△BEF，由矩形的性质得出S四边形CDFE=S△ADF+S△ABF-S△BEF=（+﹣1）S△BEF，即可得出S四边形CDFE：S△ADF值．

解：（1）①∵BE＝1，

∴CE＝BC﹣BE＝4﹣1＝3，

∵四边形ABCD是矩形，

∴∠B＝∠C＝90°，

∴∠BAE+∠BEA＝90°，

∵EF⊥AE，

∴∠AEF＝90°，

∴∠BEA+∠FEC＝90°，

∴∠BAE＝∠FEC，

∴△ABE∽△ECF，

∴＝，

即：＝，

解得：CN＝；

②过点E作EF⊥AD于F，如图1所示：

则四边形ABEF是矩形，

∴AB＝EF＝2，AF＝BE，

由折叠的性质得：CE＝C′E，CN＝C′N，∠EC′N＝∠C＝90°，

∴∠NC′D+∠EC′F＝90°，

∵∠C′ND+∠NC′D＝90°，

∴∠EC′F＝∠C′ND，

∵∠D＝∠EFC′，

∴△EC′F∽△NC′D，

∴＝＝，

∴＝＝，

∵＝，

∴＝，

∴＝＝，

∴C′D＝BE，

设BE＝x，则C′D＝AF＝x，C′F＝4﹣2x，CE＝4﹣x，

∴＝，＝，

∴DN＝x（2﹣x），CN＝，

∴CN+DN＝x（2﹣x）+＝CD＝2，

解得：x＝2或x＝，

∴BE＝2或BE＝；

（2）∵四边形ABCD为矩形，

∴BC＝AD，AD∥BC，

∴△ADF∽△EBF，

∴＝＝，

∴＝（）2＝，

∴S△ADF＝s△BEF，

S△AB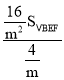F＝＝＝S△BEF，

S四边形CDFE＝S△ADF+S△ABF﹣S△BEF＝S△BEF+S△BEF﹣S△BEF＝（+﹣1）S△BEF，

∴S四边形CDFE：S△ADF＝（+﹣1）S△BEF： s△BEF＝1+﹣．