题目内容
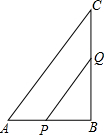
 如图,△PBQ中,BP=6,点A、C、D分别在BP、BQ、PQ上,且CD∥PB,AD∥BQ,∠QDC=∠PDA,则四边形ABCD的周长为
如图,△PBQ中,BP=6,点A、C、D分别在BP、BQ、PQ上,且CD∥PB,AD∥BQ,∠QDC=∠PDA,则四边形ABCD的周长为12
12
.分析:由CD∥PB,AD∥BQ,∠QDC=∠PDA,易证得△APD,△CDQ,△PBQ是等腰三角形,即可得四边形ABCD的周长等于BP+BQ.
解答:解:∵CD∥PB,AD∥BQ,
∴∠PDA=∠Q,∠QDC=∠P,
∵∠QDC=∠PDA,
∴∠P=∠PDA=∠QDC=∠Q,
∴PA=AD,CD=CQ,BP=BQ,
∵BP=6,
∴四边形ABCD的周长为:AB+AD+CD+BC=AB+PA+CQ+BC=BP+BQ=6+6=12.
故答案为:12.
∴∠PDA=∠Q,∠QDC=∠P,
∵∠QDC=∠PDA,
∴∠P=∠PDA=∠QDC=∠Q,
∴PA=AD,CD=CQ,BP=BQ,
∵BP=6,
∴四边形ABCD的周长为:AB+AD+CD+BC=AB+PA+CQ+BC=BP+BQ=6+6=12.
故答案为:12.
点评:此题考查了等腰三角形的性质与判定以及平行线的性质.此题难度适中,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
相关题目
 沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动:
沿边BC向点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动: B开始沿BC边向点C以2cm/s的速度移动(点Q到达点C运动停止).如果点P,Q分别从点A,B同时出发t秒(t>0)
B开始沿BC边向点C以2cm/s的速度移动(点Q到达点C运动停止).如果点P,Q分别从点A,B同时出发t秒(t>0) 如图,△PBQ中,BP=6,点A、C、D分别在BP、BQ、PQ上,且CD∥PB,AD∥BQ,∠QDC=∠PDA,则四边形ABCD的周长为________.
如图,△PBQ中,BP=6,点A、C、D分别在BP、BQ、PQ上,且CD∥PB,AD∥BQ,∠QDC=∠PDA,则四边形ABCD的周长为________.