Question

如图所示的方格图中，我们称每个小正方形的顶点为“格点”（小正方形的边长为1个单位），以格点为顶点的三角形叫做“格点三角形”．根据图形，解决下面的问题：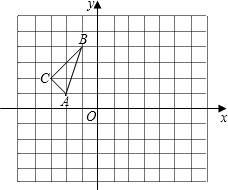
（1）格点△ABC的顶点B的坐标为

 

；
（2）画出△ABC关于y轴的对称图形；
（3）△ABC是什么三角形？为什么？

Answer 1

分析：（1）格点△ABC的顶点B的坐标由坐标系可直接得出；
（2）找出点A、B、C关于y轴的对称点A₁、B₁、C₁；连接A₁B₁、B₁C₁、A₁C₁，可得△ABC关于y轴的对称图形；
（3）由图可得，AC、BC和AB的长，根据它们的关系，可得出△ABC是直角三角形；

解答：解：（1）由图得，格点△ABC的顶点B的坐标为（-1，4）
故答案为：（-1，4）；

（2）由图得，A（-2，1）、B（-1，4）、C（-3，2），
点A、B、C关于y轴的对称点为：A₁（2，1）、B₁（1，4）、C₁（3，2），
连接A₁B₁、B₁C₁、A₁C₁，可得△ABC关于y轴的对称图形△A₁B₁C₁；

（3）由（1）得，
AC=

2

，BC=2

2

，AB=

10

，
∵AC²+BC²=10，AB²=10，
∴△ABC是直角三角形．

点评：本题考查了作图-轴对称变换，考查了轴对称图形的画图方法，熟记轴对称图形的性质定理是解答本题的基础．