题目内容
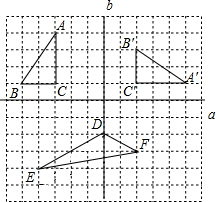
如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,解决下面的问题:(1)图中的格点△A′B′C′是由格点△ABC通过
(2)若点A坐标为(-3,4),建立符合题意的坐标系,那么△DEF中点F的坐标为
 △DEF的面积为
△DEF的面积为分析:(1)观察△A′B′C′和△ABC的位置关系可知,可以先将△ABC绕C点顺时针旋转90°,再向右平移5个单位即可;
(2)根据点A的坐标建立坐标系,可求F点的坐标,将△DEF放到一个6×2的矩形中,利用割补法求△DEF的面积.
(2)根据点A的坐标建立坐标系,可求F点的坐标,将△DEF放到一个6×2的矩形中,利用割补法求△DEF的面积.
解答: 解:(1)图中的格点△A′B′C′是由格点△ABC通过旋转和平移变换得到的;
解:(1)图中的格点△A′B′C′是由格点△ABC通过旋转和平移变换得到的;
故答案为:旋转,平移.
(2)根据A(-3,4)建立坐标系(如图),根据图形得F(2,-3),
S△DEF=6×2-
×2×4-
×2×1-
×1×6=4.
故答案为:(2,-3),4.
 解:(1)图中的格点△A′B′C′是由格点△ABC通过旋转和平移变换得到的;
解:(1)图中的格点△A′B′C′是由格点△ABC通过旋转和平移变换得到的;故答案为:旋转,平移.
(2)根据A(-3,4)建立坐标系(如图),根据图形得F(2,-3),
S△DEF=6×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(2,-3),4.
点评:本题考查了旋转的性质,点的坐标的确定方法,网格中三角形面积的计算.关键是建立坐标系,运用形数结合求解.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 23、①在如图所示的方格纸中,按下列要求画图:
23、①在如图所示的方格纸中,按下列要求画图:
 在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题:
在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”根据图形,解决下面的问题: (1)格点△ABC的顶点B的坐标为
(1)格点△ABC的顶点B的坐标为 为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.