题目内容
如图,以O为端点的射线OA所在直线的函数关系式为y= x(x≥0),射线OA上有一点M(8,y),另一点P从O点出发沿射线OA方向以每秒1个单位长度的速度运动,设运动时间为t秒,∠AOx=α.
x(x≥0),射线OA上有一点M(8,y),另一点P从O点出发沿射线OA方向以每秒1个单位长度的速度运动,设运动时间为t秒,∠AOx=α.(1)求y以及sinα、cosα的值;
(2)用含t的代数式表示点P的坐标.
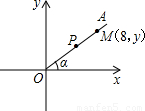
【答案】分析:(1)在函数解析式中令x=8,就可以求出y的值.因而求出几个三角函数值;
(2)作PB⊥x轴于B点,根据三角函数求PB,OB.从而得P点坐标.
解答: 解:(1)在y=
解:(1)在y= x中令x=8,解得y=6,
x中令x=8,解得y=6,
根据勾股定理得到OA=10,
∴sinα= ,cosα=
,cosα= .
.
(2)作PB⊥x轴于B点,
∵OP=t,sinα= ,
,
∴OB= t,PB=
t,PB= t,
t,
∴P( t,
t, t).
t).
点评:本题主要考查了三角函数的定义,是函数与图形相结合的问题.
(2)作PB⊥x轴于B点,根据三角函数求PB,OB.从而得P点坐标.
解答:
 解:(1)在y=
解:(1)在y= x中令x=8,解得y=6,
x中令x=8,解得y=6,根据勾股定理得到OA=10,
∴sinα=
 ,cosα=
,cosα= .
.(2)作PB⊥x轴于B点,
∵OP=t,sinα=
 ,
,∴OB=
 t,PB=
t,PB= t,
t,∴P(
 t,
t, t).
t).点评:本题主要考查了三角函数的定义,是函数与图形相结合的问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

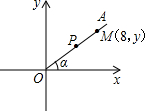 如图,以O为端点的射线OA所在直线的函数关系式为y=
如图,以O为端点的射线OA所在直线的函数关系式为y= 如图,以O为端点的射线共有多少条?( )
如图,以O为端点的射线共有多少条?( ) x(x≥0),射线OA上有一点M(8,y),另一点P从O点出发沿射线OA方向以每秒1个单位长度的速度运动,设运动时间为t秒,∠AOx=α。
x(x≥0),射线OA上有一点M(8,y),另一点P从O点出发沿射线OA方向以每秒1个单位长度的速度运动,设运动时间为t秒,∠AOx=α。