题目内容
已知∠A+∠B=90°，且cosA=
，则cosB的值为
- A.
- B.
- C.
- D.
D
分析：利用同角、互为余角的三角函数关系式求解．
解答：∵∠A+∠B=90°，
∴cosB=cos（90°-∠A）=sinA，
又∵sin2A+cos2A=1，
∴cosB=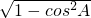
=．
故选D．
点评：本题考查了利用同角（或余角）的三角函数关系式求三角函数值．若∠A+∠B=90°，那么sinA=cosB或sinB=cosA；同角的三角函数关系式：sin2A+cos2A=1．
分析：利用同角、互为余角的三角函数关系式求解．
解答：∵∠A+∠B=90°，
∴cosB=cos（90°-∠A）=sinA，
又∵sin2A+cos2A=1，
∴cosB=
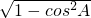=．故选D．
点评：本题考查了利用同角（或余角）的三角函数关系式求三角函数值．若∠A+∠B=90°，那么sinA=cosB或sinB=cosA；同角的三角函数关系式：sin2A+cos2A=1．
练习册系列答案
名校课堂系列答案
相关题目
22、如图，把一个三角板（AB=BC，∠ABC=90°）放入一个“U”形槽中，使三角板的三个顶点A、B、C分别槽的两壁及底边上滑动，已知∠D=∠E=90°，在滑动过程中你发现线段AD与BE有什么关系？试说明你的结论．
如图，已知∠ACB=∠BDA=90°，要使△ACB≌△BDA还需要什么条件？（请在横线上填上你认为合适的条件）
如图，在Rt△ABC中，已知，∠ACB=90°，∠B=15°，AB边的垂直平分线交AB于E，交BC于D，且BD=18cm，则AC的长是