题目内容
如图,AB⊥BD,CD⊥BD,B、D分别为垂足.

(1)已知:∠APC=90°,求证:△ABP∽△PDC.
(2)已知:AB=2,CD=3,BD=7,点P是线段BD上的一动点,若使点P分别与A、B和C、D构成的两个三角形相似,求线段PB的值.
(3)已知:AB=2,CD=3,点P是直线BD上的一动点,设PB=x,BD=y,使点P分别与A、B和C、D构成的两个三角形相似,求y关于x的函数解析式.

(1)已知:∠APC=90°,求证:△ABP∽△PDC.
(2)已知:AB=2,CD=3,BD=7,点P是线段BD上的一动点,若使点P分别与A、B和C、D构成的两个三角形相似,求线段PB的值.
(3)已知:AB=2,CD=3,点P是直线BD上的一动点,设PB=x,BD=y,使点P分别与A、B和C、D构成的两个三角形相似,求y关于x的函数解析式.
分析:(1)由于AB⊥BD,CD⊥BD,可知∠B与∠D为直角,又∠APC=90°,则∠APB+∠CPD=90°,可以得出∠A=∠CPD,从而证出△ABP∽△PDC.
(2)设PB=x,则PD为(7-x),然后分两种情况讨论:①△ABP∽△PDC;②△ABP∽△CDP.据此,即可利用相似三角形的性质列出比例式,从而求出线段PB的值.
(3)分两种情况讨论:①△ABP∽△PDC;②△ABP∽△CDP.据此,即可利用相似三角形的性质列出含x、y的比例式,从而求出y关于x的函数解析式.
(2)设PB=x,则PD为(7-x),然后分两种情况讨论:①△ABP∽△PDC;②△ABP∽△CDP.据此,即可利用相似三角形的性质列出比例式,从而求出线段PB的值.
(3)分两种情况讨论:①△ABP∽△PDC;②△ABP∽△CDP.据此,即可利用相似三角形的性质列出含x、y的比例式,从而求出y关于x的函数解析式.
解答:解:(1)证明:∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°①,
∴∠A+∠APB=90°,
又∵∠APB+∠CPD=90°,
∴∠A=∠CPD②,
∴由①②,△ABP∽△PDC.
(2)设PB=x,则PD为(7-x),
①△ABP∽△PDC时,
=
,
即
=
,
解得,(x-1)(x-6)=0,
x=1或x=6,
②△ABP∽△CDP.
=
,
即
=
,
解得x=
.
综上所述,PB=1,或PB=6,或PB=
.
(3)①△ABP∽△PDC时,
=
,
即
=
,
整理得,y=x+
;
②△ABP∽△CDP.
=
,
=
整理得,y=
x.
③△ABP∽△PDC时,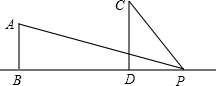
=
,
∵PD=PB-BD=x-y,
=
,
y=x-
.
∴∠B=∠D=90°①,
∴∠A+∠APB=90°,
又∵∠APB+∠CPD=90°,
∴∠A=∠CPD②,
∴由①②,△ABP∽△PDC.
(2)设PB=x,则PD为(7-x),
①△ABP∽△PDC时,
| AB |
| PD |
| BP |
| CD |
即
| 2 |
| 7-x |
| x |
| 3 |
解得,(x-1)(x-6)=0,
x=1或x=6,
②△ABP∽△CDP.
| AB |
| CD |
| BP |
| PD |
即
| 2 |
| 3 |
| x |
| 7-x |
解得x=
| 14 |
| 5 |
综上所述,PB=1,或PB=6,或PB=
| 14 |
| 5 |
(3)①△ABP∽△PDC时,
| AB |
| PD |
| BP |
| CD |
即
| 2 |
| y-x |
| x |
| 3 |
整理得,y=x+
| 6 |
| x |
②△ABP∽△CDP.
| AB |
| CD |
| BP |
| PD |
| 2 |
| 3 |
| x |
| y-x |
整理得,y=
| 5 |
| 2 |
③△ABP∽△PDC时,

| AB |
| PD |
| BP |
| CD |
∵PD=PB-BD=x-y,
| 2 |
| x-y |
| x |
| 3 |
y=x-
| 6 |
| x |
点评:本题考查了相似三角形的判定与性质,三道题步步深入,前一道题为后面的题提供思路,要注意这一点,同时题目也体现了分类讨论思想的重要作用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
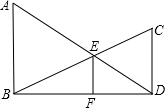 已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明
已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明
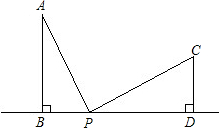 如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动,
如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在直线BD上,由B点到D点移动, 如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED.
如图,AB⊥BD于点B,ED⊥BD于点D,AE交BD于点C,且BC=DC.求证:AB=ED. 如图,AB=BD,BC=BE,∠ABD=∠EBC,则有
如图,AB=BD,BC=BE,∠ABD=∠EBC,则有 如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.
如图,AB⊥BD,CD⊥BD,AD=CB.求证:AD∥BC.