题目内容
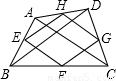
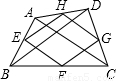
如图，已知凸四边形ABCD，E，F，G，H分别在AB，BC，CD，DA上，且BE=2AE，BF=2CF，DH=2AH，DG=2CG，求证：SKLMN=S△AKH+S△BEL+S△CFM+S△DNG．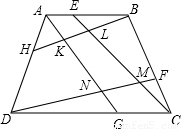
【答案】分析：由题意连接AC，得出三角形ADG的面积，然后根据图形可知
，从而进行证明．
解答：
证明：连AC，
因为DG=2GC，所以
∵BE=2AE，
∴
∴
同理，
∴S△ADC+S△BCE+S△DCF+S△ABH=S四边形ABCDS四边形ABCD=S四边形KLMN+（S△ADG-S△DGN）+（S△DCF-S△CFM）+（S△CBE-S△BEL）+（S△ABH-S△AHK）
由（1）、（2）得，S四边形KLMN=S△AHK+S△BEL+S△CFM+S△DGN
点评：此题主要考查了三角形的面积公式，用规则的图形表示出不规则的图形是解题的关键．
，从而进行证明．解答：
证明：连AC，因为DG=2GC，所以
∵BE=2AE，
∴
∴
同理，
∴S△ADC+S△BCE+S△DCF+S△ABH=S四边形ABCDS四边形ABCD=S四边形KLMN+（S△ADG-S△DGN）+（S△DCF-S△CFM）+（S△CBE-S△BEL）+（S△ABH-S△AHK）
由（1）、（2）得，S四边形KLMN=S△AHK+S△BEL+S△CFM+S△DGN
点评：此题主要考查了三角形的面积公式，用规则的图形表示出不规则的图形是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
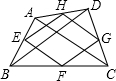如图，已知凸四边形ABCD的两对角线BD与AC之比为k，菱形EFGH各顶点位于四边形ABCD的顺次四边之上，且EF∥AC，FG∥BD，则四边形ABCD与菱形EFGH的面积之比为
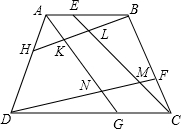如图，已知凸四边形ABCD，E，F，G，H分别在AB，BC，CD，DA上，且BE=2AE，BF=2CF，DH=2AH，DG=2CG，求证：SKLMN=S△AKH+S△BEL+S△CFM+S△DNG．
