题目内容
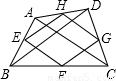
如图,已知凸四边形ABCD的两对角线BD与AC之比为k,菱形EFGH各顶点位于四边形ABCD的顺次四边之上,且EF∥AC,FG∥BD,则四边形ABCD与菱形EFGH的面积之比为 .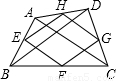
【答案】分析:设 =a,由平行线分线段成比例得出
=a,由平行线分线段成比例得出 、
、 、EH=a•BD,EF=(1-a)•AC,根据EF=EH得到
、EH=a•BD,EF=(1-a)•AC,根据EF=EH得到 的值,即求出a=
的值,即求出a= ,再代入面积公式代入即可求出四边形ABCD与菱形EFGH的面积之比.
,再代入面积公式代入即可求出四边形ABCD与菱形EFGH的面积之比.
解答:解:设 =a,则
=a,则 =1-a,
=1-a, =a,EH=a•BD,
=a,EH=a•BD,
同理:EF=(1-a)•AC,
∵菱形EFGH,
∴EF=EH,
∴a•BD=(I-a)•AC,
∴ =
= ,
,
∵ =k,
=k,
∴a= ,
,
由面积公式得: =
= ,
,
= ,
,
=
 •
• ,
,
= •
• •(k+1),
•(k+1),
= .
.
故答案为: .
.
点评:本题主要考查了面积与等积变换,平行线分线段成比例等知识点,解此题的关键是求出 和
和 的值.题型很好,但难度较大.
的值.题型很好,但难度较大.
 =a,由平行线分线段成比例得出
=a,由平行线分线段成比例得出 、
、 、EH=a•BD,EF=(1-a)•AC,根据EF=EH得到
、EH=a•BD,EF=(1-a)•AC,根据EF=EH得到 的值,即求出a=
的值,即求出a= ,再代入面积公式代入即可求出四边形ABCD与菱形EFGH的面积之比.
,再代入面积公式代入即可求出四边形ABCD与菱形EFGH的面积之比.解答:解:设
 =a,则
=a,则 =1-a,
=1-a, =a,EH=a•BD,
=a,EH=a•BD,同理:EF=(1-a)•AC,
∵菱形EFGH,
∴EF=EH,
∴a•BD=(I-a)•AC,
∴
 =
= ,
,∵
 =k,
=k,∴a=
 ,
,由面积公式得:
 =
= ,
,=
 ,
,=

 •
• ,
,=
 •
• •(k+1),
•(k+1),=
 .
.故答案为:
 .
.点评:本题主要考查了面积与等积变换,平行线分线段成比例等知识点,解此题的关键是求出
 和
和 的值.题型很好,但难度较大.
的值.题型很好,但难度较大. 
练习册系列答案
相关题目
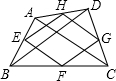 如图,已知凸四边形ABCD的两对角线BD与AC之比为k,菱形EFGH各顶点位于四边形ABCD的顺次四边之上,且EF∥AC,FG∥BD,则四边形ABCD与菱形EFGH的面积之比为
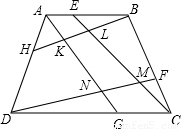
如图,已知凸四边形ABCD的两对角线BD与AC之比为k,菱形EFGH各顶点位于四边形ABCD的顺次四边之上,且EF∥AC,FG∥BD,则四边形ABCD与菱形EFGH的面积之比为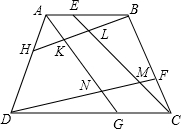 如图,已知凸四边形ABCD,E,F,G,H分别在AB,BC,CD,DA上,且BE=2AE,BF=2CF,DH=2AH,DG=2CG,求证:SKLMN=S△AKH+S△BEL+S△CFM+S△DNG.
如图,已知凸四边形ABCD,E,F,G,H分别在AB,BC,CD,DA上,且BE=2AE,BF=2CF,DH=2AH,DG=2CG,求证:SKLMN=S△AKH+S△BEL+S△CFM+S△DNG.