题目内容
17.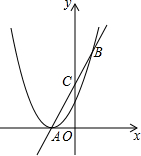 如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.
分析 (1)利用△=b2-4ac=0时,抛物线与x轴有1个交点得到4a2-4a=0,然后解关于a的方程求出a,即可得到抛物线解析式;
(2)利用点C是线段AB的中点可判断点A与点B的横坐标互为相反数,则可以利用抛物线解析式确定B点坐标,然后利用待定系数法求直线AB的解析式.
解答 解:(1)∵抛物线y=ax2+2ax+1与x轴仅有一个公共点A,
∴△=4a2-4a=0,解得a1=0(舍去),a2=1,
∴抛物线解析式为y=x2+2x+1;
(2)∵y=(x+1)2,
∴顶点A的坐标为(-1,0),
∵点C是线段AB的中点,
即点A与点B关于C点对称,
∴B点的横坐标为1,
当x=1时,y=x2+2x+1=1+2+1=4,则B(1,4),
设直线AB的解析式为y=kx+b,
把A(-1,0),B(1,4)代入得$\left\{\begin{array}{l}{-k+b=0}\\{k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=2x+2.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了利用待定系数法求函数解析式.

练习册系列答案
相关题目
7.今年9月,杭州将举办二十国集团领导人峰会,一支有着76万人的平安志愿寻访队伍,参与社会治理,成为一道亮丽的风景,其中76万人用科学记数法表示为( )人.
| A. | 7.6×106 | B. | 76×104 | C. | 7.6×105 | D. | 0.76×106 |
2. 如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
 如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
9.下表是某校合唱团成员的年龄分布
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 频数 | 5 | 15 | x | 10-x |
| A. | 平均数、中位数 | B. | 众数、中位数 | C. | 平均数、方差 | D. | 中位数、方差 |
7.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
| A. | y=-(x-$\frac{5}{2}$)2-$\frac{11}{4}$ | B. | y=-(x+$\frac{5}{2}$)2-$\frac{11}{4}$ | C. | y=-(x-$\frac{5}{2}$)2-$\frac{1}{4}$ | D. | y=-(x+$\frac{5}{2}$)2+$\frac{1}{4}$ |
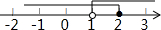
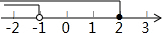


 由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形.
由一些相同的小正方体搭成的几何体的左视图和俯视图如图所示,请在网格中涂出一种该几何体的主视图,且使该主视图是轴对称图形. 从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )


