��Ŀ����
��ͼ��AB�ǰ�ԲO��ֱ��������O����AD�Ĵ��߽�����AC�ڵ�C��OC��ԲO���ڵ�E������BE��DE��
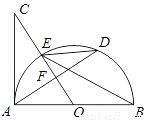
��1����Բ�İ뾶��3����EBA��30�ȣ���AD�ij��ȣ�
��2����֤����BED=��C��
��3����OA=5��AD=8��������AC�ij���
��1��AD=3����2��֤������������3��AC= �������������������1���ɴ��������ɵ�AF=DF��Ҫ��AD�ij��ȣ���Ҫ��AF�ij��ȣ��ɡ�EBA=30����Եó���FOA=60�㣬�����ó���FAO=30�㣬��֪OA�ij��Ƚ��30������ֵ���������AF�ij��ȣ��������AD�ij��ȣ���2��Ҫ֤��BED=��C��Ҫ֤����DAB=��C�����ڡ�C+��CAF=90�㣬��DAB+��CAF=90�㣬����֤������3��...
��ϰ��ϵ�д�
�����Ŀ

 ��
�� ��3.14��
��3.14�� 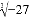 ��
�� ����6����������������( )
����6�����У�����������( )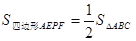 ������EPF�ڡ�ABC���ƶ���P��תʱ����E�����A��B�غϣ�������������ʼ����ȷ������� ��
������EPF�ڡ�ABC���ƶ���P��תʱ����E�����A��B�غϣ�������������ʼ����ȷ������� ��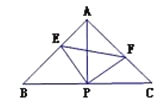
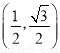 B.
B. 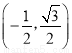 C.
C. 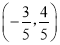 D. ��
D. �� 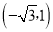
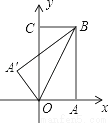
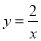 ��y��x�����������
��y��x�����������