题目内容
如图，在矩形ABCD中，AD=2，以B为圆心，BC长为半径画弧交AD于F，若
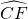长为
，．
（1）求圆心角∠CBF的度数；
（2）求图中阴影部分的面积（结果保留根号及π的形式）．
解：（1）设∠CBF的度数为n°，
由
，得
．
所以
，即∠CBF=60°．
（2）由∠ABC=90°，∠FBC=60°，
得∠ABF=30°．
在Rt△ABF中，
，
，
所以FD=AD-AF=1．
，
所以S阴影=S梯形DFBC-S扇形BCF=
．
分析：（1）根据弧长公式，即可求得∠CBF的度数；
（2）根据（1）的结论，求得∠ABF=30°．再根据直角三角形的性质可以求得AB、AF的长，从而求得DF的长．则阴影部分的面积等于梯形BCDF的面积减去扇形BCF的面积．
点评：熟练运用弧长公式和扇形的面积公式，掌握直角三角形的性质．30°所对的直角边是斜边的一半．
由
，得．所以
，即∠CBF=60°．（2）由∠ABC=90°，∠FBC=60°，
得∠ABF=30°．
在Rt△ABF中，
，，所以FD=AD-AF=1．
，所以S阴影=S梯形DFBC-S扇形BCF=
．分析：（1）根据弧长公式
，即可求得∠CBF的度数；（2）根据（1）的结论，求得∠ABF=30°．再根据直角三角形的性质可以求得AB、AF的长，从而求得DF的长．则阴影部分的面积等于梯形BCDF的面积减去扇形BCF的面积．
点评：熟练运用弧长公式和扇形的面积公式，掌握直角三角形的性质．30°所对的直角边是斜边的一半．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
如图，在矩形ABCD中，AB=4cm，BC=8cm，点P从点A出发以1cm/s的速度向点B运动，点Q从点B出发以2cm/s的速度向点C运动，设经过的时间为xs，△PBQ的面积为ycm2，则下列图象能反映y与x之间的函数关系的是（ ）
．
动过程中，Q点停留了1s，图②是P、Q两点在折线AB-BC-CD上相距的路程S（cm）与时间t（s）之间的函数关系图象．
如图，在矩形ABCD中，对角线AC，BD相交于点O，∠AOB=60°，AB=6，则AD=（ ）
DE，EF与AB交于点F，设CE=x，BF=y．