题目内容
如图，面积为12cm2的△ABC沿着BC方向平移到△DEF的位置，平移距离是边BC长的两倍，则图中四边形ABED的面积为（ ）分析：设点A到BC的距离为h，根据三角形的面积列出等式，再根据平移的性质判定出四边形ABED是平行四边形，然后根据平行四边形的面积公式列式计算即可得解．
解答：解：设点A到BC的距离为h，
则S△ABC=
BC•h=12，
所以，BC•h=24cm2，
∵△DEF是△ABC平移得到，
∴四边形ABED是平行四边形，
∵平移距离是BC的2倍，
∴BE=2BC，
∴四边形ABED的面积=BE•h=2BC•h=2×24=48cm2．
故选C．
则S△ABC=
| 1 |
| 2 |
所以，BC•h=24cm2，
∵△DEF是△ABC平移得到，
∴四边形ABED是平行四边形，
∵平移距离是BC的2倍，
∴BE=2BC，
∴四边形ABED的面积=BE•h=2BC•h=2×24=48cm2．
故选C．
点评：本题考查了平移的性质，平行四边形的判定与性质，根据三角形的面积公式求出BC•h的值是解题的关键．
练习册系列答案
相关题目
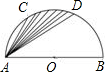如图，AB为半圆O的直径，点C、D是半圆的三等分点，AB=12cm，则由弦AC、AD和
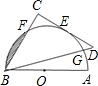于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．
所围成的阴影部分的面积为 cm2．
的△ABC沿BC方向平移至△DEF的位置， 平移的距离是边BC长的两倍，则图中的四边形ACED的面积为 ( )
(A)24 cm。 (B)36 cm2