题目内容
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为直线
为直线![]() 上一动点,以
上一动点,以![]() 为直角边且在
为直角边且在![]() 的右侧作等腰直角三角形
的右侧作等腰直角三角形![]() ,
,![]() ,
,![]() .
.

(1)如果![]() ,
,![]() .
.
①当点![]() 在线段
在线段![]() 上时,如图1,线段
上时,如图1,线段![]() 、
、![]() 的位置关系为___________,数量关系为_____________
的位置关系为___________,数量关系为_____________
②当点![]() 在线段
在线段![]() 的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动。探究:当
上运动。探究:当![]() 多少度时,
多少度时,![]() ?小明通过(1)的探究,猜想
?小明通过(1)的探究,猜想![]() 时,
时,![]() .他想过点
.他想过点![]() 做
做![]() 的垂线,与
的垂线,与![]() 的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
的延长线相交,构建图2的基本图案,寻找解决此问题的方法。小明的想法对吗?如不对写出你的结论;如对按此方法解决问题并写出理由.
【答案】(1)①垂直,相等;②都成立;(2)当![]() 时,
时,![]()
【解析】
(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;
②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;
(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.
解:(1)①CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,
∴∠BAD=∠CAE.
又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS)
∴∠ACE=∠B=45°且 CE=BD.
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即 CE⊥BD.
故答案为:垂直,相等;
②都成立
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
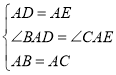
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ;
;
(2)当![]() 时,
时,![]() (如图).
(如图).

理由:过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
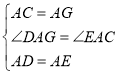
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.