题目内容
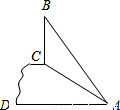
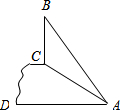 如图,斜坡AC=8米,∠CAD=30°.坡顶有一旗杆BC(旗杆与地面AD垂直),旗杆顶端B点与A点有一彩带AB相连,AB=10米.试求旗杆BC的高度?(结果保留根号)
如图,斜坡AC=8米,∠CAD=30°.坡顶有一旗杆BC(旗杆与地面AD垂直),旗杆顶端B点与A点有一彩带AB相连,AB=10米.试求旗杆BC的高度?(结果保留根号)
 解:延长BC交AD于点E,则CE⊥AD,∠CAD=30°,AC=8,
解:延长BC交AD于点E,则CE⊥AD,∠CAD=30°,AC=8,则CE=4,AE=4
 ,(4分)
,(4分)在Rt△BAE中,BE=
 ,(6分)
,(6分)所以BC=BE-CE=(2
 -4)米.(8分)
-4)米.(8分)分析:如果延长BC交AD于E点,则CE⊥AD,要求BC的高度,就要知道BE和CE的高度,就要先求出AE的长度.直角三角形ACE中有坡比,由AC的长,那么就可求出AE的长,然后求出BE、CE的高度,BC=BE-CE,即可得出结果.
点评:本题考查了勾股定理的应用,两个直角三角形有公共的直角边,先求出公共边的解决此类题目的基本出发点.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
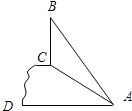 如图,斜坡AC的坡度(坡比)为1:
如图,斜坡AC的坡度(坡比)为1: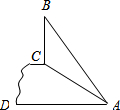 如图,斜坡AC=8米,∠CAD=30°.坡顶有一旗杆BC(旗杆与地面AD垂直),旗杆顶端B点与A点有一彩带AB相连,AB=10米.试求旗杆BC的高度?(结果保留根号)
如图,斜坡AC=8米,∠CAD=30°.坡顶有一旗杆BC(旗杆与地面AD垂直),旗杆顶端B点与A点有一彩带AB相连,AB=10米.试求旗杆BC的高度?(结果保留根号)