Question

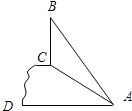（2012•金牛区三模）如图，斜坡AC的坡度（坡比）为1：

3

，AC=15米，坡顶有一旗杆BC，旗杆顶端B点与A点有一条彩带AB相连，AB=21米，试求旗杆BC的高度．

Answer 1

分析：如果延长BC交AD于E点，则CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的长度．直角三角形ACE中有坡比，由AC的长，那么就可求出AE的长，然后求出BE、CE的高度，BC=BE-CE，即可得出结果．

解答：解：延长BC交AD于E点，则CE⊥AD．
∵在Rt△AEC中，AC=15米，由坡比为1：

3

可知：∠CAE=30°，
∴CE=AC•sin30°=15×

1

2

=7.5米，
AE=AC•cos30°=15×

3

2

=7.5

3

米，
在Rt△ABE中，BE=

AB2-AE2

=16.5米，
∵BE=BC+CE，
∴BC=BE-CE=16.5-7.5=9（米）．
答：旗杆BC的高度为9米．

点评：考查了解直角三角形的应用-坡度坡角问题．两个直角三角形有公共的直角边，先求出公共边的长是解决此类题目的基本出发点．