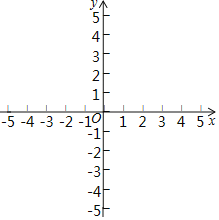题目内容
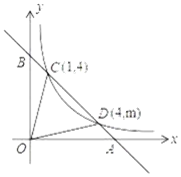
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)双曲线上是否存在一点P,使得△POC和△POD的面积相等?若存在,给出证明并求出点P的坐标;若不存在,说明理由.
【答案】(1)y= ![]() ,m=1;(2)P(2,2)或P(﹣2,﹣2),理由见解析.
,m=1;(2)P(2,2)或P(﹣2,﹣2),理由见解析.
【解析】
(1)把C(1,4)代入y=![]() 求出k=4,把(4,m)代入y=
求出k=4,把(4,m)代入y=![]()
![]() 求出m即可,把C(1,4),D(4,1)代入y=ax+b得出解析式,求得出一次函数的解析式;(2)双曲线上存在点P,使得S△POC=S△POD,这个点就是∠COD的平分线与双曲线的y=
求出m即可,把C(1,4),D(4,1)代入y=ax+b得出解析式,求得出一次函数的解析式;(2)双曲线上存在点P,使得S△POC=S△POD,这个点就是∠COD的平分线与双曲线的y=![]() 交点,易证△POC≌△POD,则S△POC=S△POD.
交点,易证△POC≌△POD,则S△POC=S△POD.
(1)把C(1,4)代入y=![]() ,得k=4,
,得k=4,
把(4,m)代入y= ![]() ,得m=1;
,得m=1;
∴反比例函数的解析式为y= ![]() ,m=1;
,m=1;
把C(1,4),D(4,1)代入y=ax+b得出![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=﹣x+5;
(2)双曲线上存在点P(2,2),使得S△POC=S△POD,理由如下:
∵C点坐标为:(1,4),D点坐标为:(4,1),
∴OD=OC=![]() ,
,
∴当点P在∠COD的平分线上时,∠COP=∠POD,又OP=OP,
∴△POC≌△POD,∴S△POC=S△POD.
∵C点坐标为:(1,4),D点坐标为:(4,1),
可得∠COB=∠DOA,
又∵这个点是∠COD的平分线与双曲线的y=![]() 交点,
交点,
∴∠BOP=∠POA,
∴P点横纵坐标坐标相等,
即xy=4,x2=4,∴x=±2,
∵x>0,
∴x=2,y=2,
故P点坐标为(2,2),使得△POC和△POD的面积相等.
利用点CD关于直线y=x对称,P(2,2)或P(﹣2,﹣2).

【题目】阅读下列内容,并解答问题.
一个滑雪者从山坡滑下,为了得出滑行距离![]() (单位:
(单位:![]() )与滑行时间
)与滑行时间![]() (单位:
(单位:![]() )之间的关系式,测得一些数据(如表):
)之间的关系式,测得一些数据(如表):
滑行时间 | 0 | 1 | 2 | 4 | 5 |
滑行距离 | 0 | 4.5 | 14 | 28.5 | 48 |
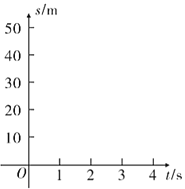
为观察![]() 与
与![]() 之间的关系,建立坐标系(如图),以
之间的关系,建立坐标系(如图),以![]() 为横坐标,
为横坐标,![]() 为纵坐标.请解答以下问题:
为纵坐标.请解答以下问题:
(1)描出表中数据对应的5个点,并用平滑曲线连接它们;
(2)根据(1)所画出的曲线图象,利用我们所学的函数,近似地表示![]() 关于
关于![]() 的函数关系式.
的函数关系式.