Question

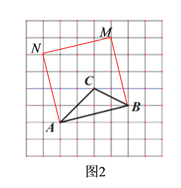
【题目】如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．

（1）计算AC2+BC2的值等于　 　；

（2）请在如图所示的网格中，用无刻度的直尺，画出一个平行四边形ABEF，使得该平行四边形的面积等于16；

（3）请在如图所示的网格中，用无刻度的直尺，画出一个矩形ABMN，使得该矩形的面积等于AC2+BC2．

Answer 1

【答案】（1）13；（2）见解析（3）见解析

【解析】分析：

（1）结合图形，由勾股定理分别计算出AC2和BC2，再求两者的和即可；

（2）由图可知，点A到点B的水平距离为4，结合S平行四边形ABEF=16可知，BE=FA=4，由此即可画出图形如下图1所示；

（3）由图易得AB=，结合S矩形ABMN= AC2+BC2=13可知AN=BM=，即矩形ABMN是正方形，由此即可画出图形如下图2所示；

详解：

（1）如图1，∵AC2=22+22=8，BC2=22+12=5，

∴AC2+BC2=8+5=13；

（2）如下图1所示，图中的平行四边形ABEF为所求平行四边形；

（3）如下图2所示，图中的矩形ABMN为所求矩形；