题目内容
【题目】正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
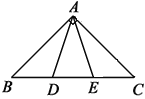
(1)如图,若tanB=2,则![]() 的值为
的值为
(2)将△ABC绕点D旋转得到△A′B′C′,连接BB′、CC′.若![]() , 则tanB的值为
, 则tanB的值为 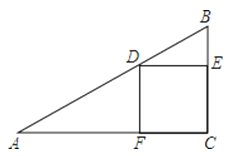
【答案】![]() ;
;![]()
【解析】解:(1)∵四边形CEDF为正方形,
∴ED=EC,∠CED=90°,
在Rt△BDE中,∵tanB=![]() =2,
=2,
∴DE=2BE,
∴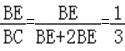
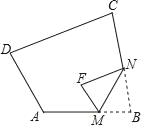
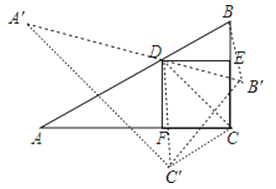
(2)连结DC、DC′,如图,
∵△ABC绕点D旋转得到△A′B′C′,
∴DB=DB′,DC=DC′,∠BDB′=∠CDC′,
即![]()
∴△DBB′∽△DCC′,
∴![]() =
=![]()
设DC=3![]() x,BD=5x,
x,BD=5x,
∵四边形CEDF为正方形,
∴DE=3x,
在Rt△BDE中,BE=![]()
∴tanB=![]()
所以答案是![]() ,
, ![]() .
. 
(1)由正方形的性质得ED=EC,∠CED=90°,再在Rt△BDE中,利用正切的定义得到DE=2BE,则CE=BE,所以![]() =
=![]() ;
;
(2)连结DC、DC′,如图,根据旋转的性质得DB=DB′,DC=DC′,∠BDB′=∠CDC′,则可判断△DBB′∽△DCC′,根据相似三角形的性质得![]() =
=![]() , 则可设DC=3
, 则可设DC=3![]() x,BD=5x,然后利用正方形性质得DE=3x,接着利用勾股定理计算出BE=4x,最后根据正切的定义求解.
x,BD=5x,然后利用正方形性质得DE=3x,接着利用勾股定理计算出BE=4x,最后根据正切的定义求解.
【考点精析】本题主要考查了相似三角形的判定与性质的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.

练习册系列答案
相关题目