题目内容
14.计算或化简:(1)a•(-2a+1)-(2a)2
(2)(-2xy)2•2x2y+(-2x2y)3÷(2x2)
(3)(-2)2+(3.14-π)0+(-2)-3
(4)(x-2y)2-(2x-3)(-2x-3)
(5)(x-8)(x+5)-(2x-1)(x+2)
(6)$\frac{{x}^{2}-10x+25}{x-1}$÷$\frac{5-x}{{x}^{2}-1}$.
分析 (1)直接利用单项式乘以多项式以及积的乘方运算法则化简求出答案;
(2)直接利用积的乘方运算法则和整式除法运算法则化简求出答案;
(3)利用负指数幂的性质以及零指数幂的性质分别化简求出答案;
(4)利用乘法公式计算得出答案;
(5)利用多项式乘以多项式运算法则计算得出答案;
(6)直接分解因式,再利用分式的性质化简即可.
解答 解:(1)a(-2a+1)-(-2a)2
=-2a2+a-4a2,
=-6a2+a;
(2)原式═4x2y2*2x2y-8x6y3÷2x2
=8x4y3-4 x4y3
=4x4y3;
(3)(-2)2+(2011-$\sqrt{3}$)0-(-2)-3
=4+1-$\frac{1}{8}$
=4$\frac{7}{8}$;
(4)原式=x2-4xy+4y2-(9-4x2)
=x2-4xy+4y2-9+4x2
=5x2-4xy+4y2-9;
(5)原式=x2-3x-40-(2x2+3x-2)
=x2-3x-40-2x2-3x+2
=-x2-6x-38;
(6)原式=$\frac{(x-5)^{2}}{x-1}$×$\frac{(x+1)(x-1)}{5-x}$
=(5-x)(x+1).
点评 此题主要考查了分式的乘除运算以及积的乘方运算、乘法公式的应用,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
4.以下列各组数据为边长,能构成三角形的是( )
| A. | 4,4,10 | B. | 4,5,9 | C. | 3,10,4 | D. | 3,6,5 |
2.下列调查中,最适合采用抽样调查的是( )
| A. | 调查我市居民对汽车废气污染环境的看法 | |
| B. | 对全班同学的身高情况进行调查 | |
| C. | 乘坐高铁对旅客的行李的检查 | |
| D. | 对学校的卫生死角进行调查 |
19.弹簧挂上适当的重物后会按一定的规律伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表
(1)如表反映了哪两个变量之间的关系?哪个是自变量?
(2)写出x与y之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度.
| 所挂物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧的长度y(cm) | 15 | 15.6 | 16.2 | 16.8 | 17.4 | 18 | 18.6 |
(2)写出x与y之间的关系式;
(3)当物体的质量逐渐增加时,弹簧的长度怎样变化?
(4)当所挂物体的质量为11.5kg时,求弹簧的长度.
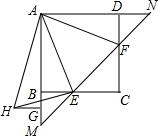 如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.
如图,在矩形ABCD中,点E、F分别在边BC、CD上,且EF分别与AB、AD的延长线交于点M、N,∠EAF=∠CEF=45°.点G在边AB的延长线上,将△ADF绕着点A按顺时针方向旋转90°后能与△AGH重合,连接EH.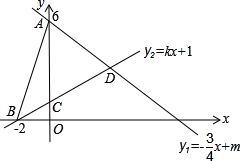 如图,直线l1:y1=-$\frac{3}{4}$x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
如图,直线l1:y1=-$\frac{3}{4}$x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.