题目内容
(本题12分)如图,△ABC和△CDE均为等腰三角形,AC=BC,CD=CE,AC>CD,∠ACB=∠DCE且点A、D、E在同一直线上,连接BE.
(1)若∠ACB=60°, 则∠AEB的度数为 ;
线段AD、BE之间的数量关系是 .
(2)若∠ACB=∠DCE=90°, CM为△DCE中DE边上的高.
①求∠AEB的度数.
②若 ,
, ,试求CM的长.(请写全必要的证明和计算过程)
,试求CM的长.(请写全必要的证明和计算过程)

(1)60°,AD=BE;
(2)①∠AEB =90°,
②在CM= 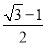
【解析】
试题分析:(1)∵∠ACB=∠DCE,∠CDB=∠CDB,
∴∠ACD=∠BCE
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠ADC=∠BEC,AD=BE
若∠ACB=60°,则△ABC和△CDE均为等边三角形,∠ADC=120°,从而∠BEC =120°,∠AEB =60°
故答案为:60°,AD=BE;
(2)①∵∠ACB=∠DCE,∠CDB=∠CDB,
∴∠ACD=∠BCE
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS)
∴∠ADC=∠BEC,AD=BE
若∠ACB=90°,则△ABC和△CDE均为等腰直角三角形,∠ADC=135°,从而∠BEC =135°,∠AEB =135°-45°=90°,
②在等腰直角△ABC中,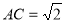 ,由勾股定理知:AB=2,
,由勾股定理知:AB=2,
在等腰直角△AEB中,因为BE=1, AB=2,由勾股定理知:AE=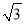 ,
,
又因为AD=BE=1,所以DE=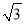 -1,
-1,
因为△CDE均为等腰直角三角形,CM为△DCE中DE边上的高,
所以CM= 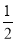 DE=
DE=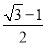
考点:1.等腰三角形的性质2.勾股定理3.三角形的全等的判定及性质

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的方程
的方程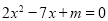 的两实数根互为倒数,那么
的两实数根互为倒数,那么 的值为( )
的值为( ) B.
B. C.2 D.
C.2 D.

 元,又从另一个鱼摊买了两条鱼,平均每条
元,又从另一个鱼摊买了两条鱼,平均每条 元,后来他又以每条
元,后来他又以每条 元的价格把鱼全部卖给了乙,结果发现赔了钱,原因是 ( )
元的价格把鱼全部卖给了乙,结果发现赔了钱,原因是 ( ) B.
B.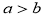 C.
C. D.与
D.与 和
和 大小无关
大小无关 为
为 ,则输出
,则输出 的结果为____________。
的结果为____________。
 (配方法);
(配方法); (公式法).
(公式法).