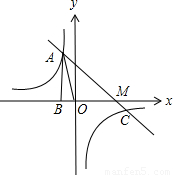
题目内容
 已知反比例函数
已知反比例函数 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为2,若直线AC经过点A,并且经过反比例函数
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为2,若直线AC经过点A,并且经过反比例函数 的图象上另一点C(n,
的图象上另一点C(n, ).
).
(1)反比例函数的解析式为______,m=______,n=______;
(2)求直线AC的解析式;
(3)在y轴上是否存在一点P,使△PAO为等腰三角形?若存在,请求出P点坐标;若不存在,说明理由.
 解:(1)∵Rt△AOB面积为2,
解:(1)∵Rt△AOB面积为2,∴|k|=4,
则反比例函数的解析式是:y=-
 ;
;把A(-2,m)代入y=-
 得,m=-
得,m=- =2;
=2;把C(n,
 )代入y=
)代入y= 得:-
得:- =-
=- ,解得:n=
,解得:n= ;
;(2)设直线AC的解析式为y=ax+b,由(1)知A(-2,2),C(
 ,-
,- )
)∵直线AC经过点A、B
∴

解得

∴直线AC的解析式y=
 x+
x+ .
.(3)答:存在点P使△PAO为等腰三角形;
∵点A(-2,2),AB=|2|=2,
∴OB=|-2|=2,在Rt△AOB中,OA=
 =2
=2 .
.①以点O为圆心,以OA长为半径画弧,交y轴于点P1、P2,P1(0,-2
 ),P2(0,2
),P2(0,2 ).(如图1)
).(如图1)②以点A为圆心,以OA长为半径画弧,交y轴于点P3、另一个交点与点O重合.由勾股定理算得P3(0,4).(如图1)
③作OA的垂直平分线l交y轴于P4,如图2,
∵AB=OB=2,∠ABO=90°,∴∠BOA=45°,∴∠P4OA=45°
∵直线l是OA的垂直平分线,∴∠P4KO=90°,OK=
 OA.
OA.∴∠KP4O=45°,OK=
 =
= ,∠P4OA=∠KP4O,OK=KP4=
,∠P4OA=∠KP4O,OK=KP4= .
.∴由勾股定理求得OP4=2.点P4(0,2).
综上可知:满足条件的点P的坐标分别为:P1(0,-2
 ),P2(0,2
),P2(0,2 ),P3(0,4),P4(0,2).
),P3(0,4),P4(0,2).分析:(1)根据反比例函数式比例系数k的意义即可求得k的值,然后把A,C的坐标代入反比例函数的解析式即可求得m,n的值;
(2)利用待定系数法即可求得函数的解析式;
(3)存在点P使△PAO为等腰三角形,分O点、A点和P点是等腰三角形的顶点三种情况进行讨论,利用勾股定理以及垂直平分线的性质即可求解.
点评:本题考查反比例函数和一次函数解析式的确定、图形的面积求法、等腰三角形的判定等知识及综合应用知识、解决问题的能力.要注意(3)在不确定等腰三角形的腰和底的情况下要考虑到所有的情况,不要漏解.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
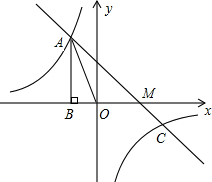 面积为3,若直线y=ax+b经过点A,并且经过反比例函数
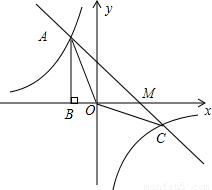
面积为3,若直线y=ax+b经过点A,并且经过反比例函数 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)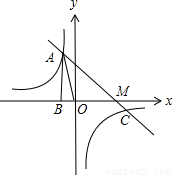
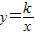 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数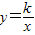 的图象上另一点C(n,-
的图象上另一点C(n,- ),
),
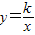 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)
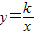 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)