题目内容
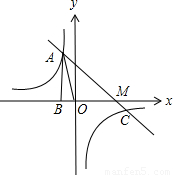
已知反比例函数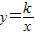 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数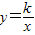 的图象上另一点C(n,-
的图象上另一点C(n,- ),
),(1)求反比例函数的解析式和直线y=ax+b解析式;
﹙2﹚求△AOC的面积;
(3)在坐标轴上是否存在一点P,使△PAO为等腰三角形?若存在,请直接写出P点坐标;若不存在,说明理由.
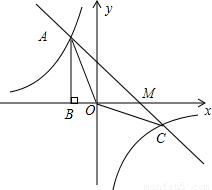
【答案】分析:(1)根据△AOB的面积求出A点的坐标,然后根据A点坐标确定出反比例函数的解析式.进而求得C点的坐标.根据C、A的坐标即可求得直线AC的解析式;
(2)将△AOC分成△AOM和COM两部分进行求解.先根据直线AC的解析式求出M的坐标,即可得出OM的长,然后根据A、C的纵坐标即可求出△AOC的面积;
(3)以O为圆心,OA为半径,交坐标轴于四点,这四点均符合点P的要求.以A为圆心,AO为半径,交坐标轴于两点,作AO的垂直平分线,交坐标轴于两点,因此共有8个符合要求的点.
解答:解:
(1)在Rt△OAB中,OB=2,S△OAB=3,
∴AB=3,
即A(-2,3),
∴反比例函数的解析式为y=- ,
,
∴C(4,- ),
),
设直线AC的解析式为y=kx+b,则有:
 ,
,
解得: ,
,
∴y=- x+
x+ ;
;
(2)根据(1)y=- x+
x+ ,
,
得M(2,0),
∴OM=2,
∴S△AOC=S△AOM+S△OCM= ×2×3+
×2×3+ ×2×
×2× =4.5;
=4.5;
(3)存在.
∵A(-2,3),
∴OA= ,
,
当OA=OP时,P1(0, )、P2(
)、P2( ,0)、P3(0,
,0)、P3(0, )、P4(
)、P4( ,0);
,0);
当OA=AP时,P5(0,6)、P6(-4,0);
当AP=OP时,P7(0, )、P8(-
)、P8(- ,0).
,0).
点评:本题考查反比例函数和一次函数解析式的确定、图形的面积求法、等腰三角形的判定等知识及综合应用知识、解决问题的能力.要注意(3)在不确定等腰三角形的腰和底的情况下要考虑到所有的情况,不要漏解.
(2)将△AOC分成△AOM和COM两部分进行求解.先根据直线AC的解析式求出M的坐标,即可得出OM的长,然后根据A、C的纵坐标即可求出△AOC的面积;
(3)以O为圆心,OA为半径,交坐标轴于四点,这四点均符合点P的要求.以A为圆心,AO为半径,交坐标轴于两点,作AO的垂直平分线,交坐标轴于两点,因此共有8个符合要求的点.
解答:解:
(1)在Rt△OAB中,OB=2,S△OAB=3,
∴AB=3,
即A(-2,3),
∴反比例函数的解析式为y=-
 ,
,∴C(4,-
 ),
),设直线AC的解析式为y=kx+b,则有:
 ,
,
解得:
 ,
,∴y=-
 x+
x+ ;
;(2)根据(1)y=-
 x+
x+ ,
,得M(2,0),
∴OM=2,
∴S△AOC=S△AOM+S△OCM=
 ×2×3+
×2×3+ ×2×
×2× =4.5;
=4.5;(3)存在.
∵A(-2,3),
∴OA=
 ,
,当OA=OP时,P1(0,
 )、P2(
)、P2( ,0)、P3(0,
,0)、P3(0, )、P4(
)、P4( ,0);
,0);当OA=AP时,P5(0,6)、P6(-4,0);
当AP=OP时,P7(0,
 )、P8(-
)、P8(- ,0).
,0).点评:本题考查反比例函数和一次函数解析式的确定、图形的面积求法、等腰三角形的判定等知识及综合应用知识、解决问题的能力.要注意(3)在不确定等腰三角形的腰和底的情况下要考虑到所有的情况,不要漏解.

练习册系列答案
相关题目
 图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB
图象过第二象限内的点A(-2,m)AB⊥x轴于B,Rt△AOB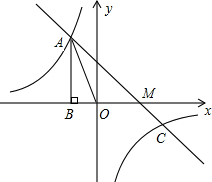 面积为3,若直线y=ax+b经过点A,并且经过反比例函数
面积为3,若直线y=ax+b经过点A,并且经过反比例函数 ),
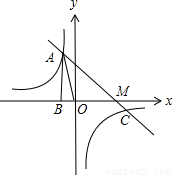
), 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)
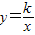 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)
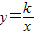 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)