题目内容
等边三角形边长为a，则这个三角形外接圆面积为
- A.πa2
- B.
- C.
- D.
C
分析：根据题意画出图形，由垂径定理求出∠AD的长，由等边三角形外接圆的性质求出∠DAO的度数，进而得出OA的长，从而得出结论．
解答：
解：∵等边三角形的边长为a，
∴AD=
，
∵∠DAO=
∠BAC=×60°=30°，
∴OA=
=
=
a，
∴这个三角形外接圆面积=（a）2π=
πa2．
故选C．
点评：本题考查的是三角形的外接圆与外心及等边三角形的性质，根据题意画出图形，利用数形结合求解是解答此题的关键．
分析：根据题意画出图形，由垂径定理求出∠AD的长，由等边三角形外接圆的性质求出∠DAO的度数，进而得出OA的长，从而得出结论．
解答：
解：∵等边三角形的边长为a，∴AD=
，∵∠DAO=
∠BAC=×60°=30°，∴OA=
==a，∴这个三角形外接圆面积=（
a）2π=πa2．故选C．
点评：本题考查的是三角形的外接圆与外心及等边三角形的性质，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
等边三角形边长为a，则该三角形的面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
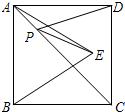6、如图所示，正方形ABCD，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，最小值为5，则正方形边长为（ ）
等边三角形边长为1厘米，分别以每边为直径向三角形内侧作半圆，交成的阴影部分（即这些半圆的公共部分）的面积是