Question

等边三角形边长为1厘米，分别以每边为直径向三角形内侧作半圆，交成的阴影部分（即这些半圆的公共部分）的面积是

π- 3

8

平方厘米（如图）（用准确式子表示结果）

Answer 1

分析：根据图形可知，利用三个扇形面积减去2△DEF面积即是阴影部分面积．

解答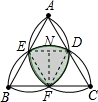：解：设三个半圆相交于点E，F，D，连接ED，DF，DE，作FN⊥ED，
∵等边三角形边长为1厘米，分别以每边为直径向三角形内侧作半圆，
∴半圆半径为：

1

2

，
ED=EF=DF=

1

2

，
∴△EFD为等边三角形，
∴扇形EFD面积为：

60π×( 1 2 )2

360

=

1

24

π，
∴三个扇形面积为：

π

8

，
∵ED=EF=DF=

1

2

，
∴ND=

1

4

，NF=

3

4

，
∴S_△DEF=

1

2

×

1

2

×

3

4

=

3

16

，
∴阴影部分（即这些半圆的公共部分）的面积是：扇形EDF+扇形EFD+扇形DEF-2S_△DEF=

π

8

-

3

8

=

π- 3

8

，
故答案为：

π- 3

8

．

点评：此题主要考查了扇形面积求法，根据已知得出三个扇形面积减去2△DEF面积即是阴影部分面积是解题关键．