题目内容
4.求|x+1|+|x-2|+|x+3|+|x-7|的最小值及此时x的取值范围.分析 要求原代数式的最小值,需化去绝对值,只需对x的取值进行分类讨论,就可解决问题.
解答 解:∵当x≤-3时,原式=-x-1-x+2-x-3-x+7=-4x+5,此时最小值为原式=-4×(-3)+5=17,
当x≥7时,原式=x+1+x-2+x+3+x-7=4x-5,此时最小值为原式=4×7-5=23,
当-3≤x≤-1时,原式=-x-1-x+2+x+3-x+7=-2x+11,此时最小值为x=-1时,-2×(-1)+11=13,
当-1≤x≤2时,原式=x+1-x+2+x+3-x+7=13,此时最小值为13,
当2≤x≤7时,原式=x+1+x-2+x+3-x+7=2x+9,此时最小值为x=2时,2×2+9=13,
∴当-1≤x≤2时,有最小值13.
点评 本题考查了绝对值的化简、不等式的性质等知识,还考查了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 如图,△ABC和△DBE为等腰直角三角形,且AD=2,AE=2$\sqrt{3}$,求AC的长.
如图,△ABC和△DBE为等腰直角三角形,且AD=2,AE=2$\sqrt{3}$,求AC的长.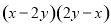 B.
B. 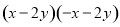
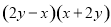 D.
D.