题目内容
计算或解方程:
(1) ;
;
(2)2cos60°+2sin30°+4tan45°;
(3)(x-1)2=2(x-1);
(4)x2+3=2(x+2);
(5) .
.
解:(1)原式= -4×
-4× -
- +1+2
+1+2 =
= +1-2
+1-2 -
- +1+2
+1+2 =2;
=2;
(2)原式=2× +2×
+2× +4×1=6;
+4×1=6;
(3)∵(x-1)2=2(x-1),
∴(x-1)(x-1-2)=0,
∴x1=1,x2=3;
(4)∵x2+3=2(x+2),
∴x2-2x+1=2,
∴(x-1)2=± ,
,
∴x1=1+ ,x2=1-
,x2=1- ;
;
(5)原式=(1+1)×tan6°× =2.
=2.
分析:(1)利用cos30°= 、sin45°=
、sin45°= 、
、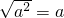 (a≥0)计算即可;(2)利用cos60°=sin30°=
(a≥0)计算即可;(2)利用cos60°=sin30°= 、tan45°=1计算即可;(3)利用提取公因式个方法解方程即可;(4)利用配方法解方程即可;(5)利用互余的两个角的正切之积等于1;相等两角的正弦平方与余弦平方和等于1;任意一个锐角的正弦除以余弦等于它的正切;互余的两个锐角,其中一个角的正切等于另一个角的余切计算即可.
、tan45°=1计算即可;(3)利用提取公因式个方法解方程即可;(4)利用配方法解方程即可;(5)利用互余的两个角的正切之积等于1;相等两角的正弦平方与余弦平方和等于1;任意一个锐角的正弦除以余弦等于它的正切;互余的两个锐角,其中一个角的正切等于另一个角的余切计算即可.
点评:本题考查实数的综合运算能力、解一元二次方程,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.注意配方法、提公因式方法的利用.
 -4×
-4× -
- +1+2
+1+2 =
= +1-2
+1-2 -
- +1+2
+1+2 =2;
=2;(2)原式=2×
 +2×
+2× +4×1=6;
+4×1=6;(3)∵(x-1)2=2(x-1),
∴(x-1)(x-1-2)=0,
∴x1=1,x2=3;
(4)∵x2+3=2(x+2),
∴x2-2x+1=2,
∴(x-1)2=±
 ,
,∴x1=1+
 ,x2=1-
,x2=1- ;
;(5)原式=(1+1)×tan6°×
 =2.
=2.分析:(1)利用cos30°=
 、sin45°=
、sin45°= 、
、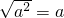 (a≥0)计算即可;(2)利用cos60°=sin30°=
(a≥0)计算即可;(2)利用cos60°=sin30°= 、tan45°=1计算即可;(3)利用提取公因式个方法解方程即可;(4)利用配方法解方程即可;(5)利用互余的两个角的正切之积等于1;相等两角的正弦平方与余弦平方和等于1;任意一个锐角的正弦除以余弦等于它的正切;互余的两个锐角,其中一个角的正切等于另一个角的余切计算即可.
、tan45°=1计算即可;(3)利用提取公因式个方法解方程即可;(4)利用配方法解方程即可;(5)利用互余的两个角的正切之积等于1;相等两角的正弦平方与余弦平方和等于1;任意一个锐角的正弦除以余弦等于它的正切;互余的两个锐角,其中一个角的正切等于另一个角的余切计算即可.点评:本题考查实数的综合运算能力、解一元二次方程,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算.注意配方法、提公因式方法的利用.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目