Question

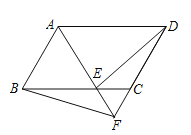
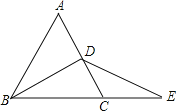
【题目】已知△ABC为等边三角形，BD为中线，延长BC至E，使CE=CD=1，连接DE，求DE的长.

Answer 1

【答案】DE=

【解析】

根据等边三角形的性质可得∠ABC=∠ACB=60°，AC=BC，∠DBC=∠ABC=30°，∠BDC=90°，AD=CD=AC，再证明∠E=30°=∠DBC，根据等腰三角形的性质可得BD=DE，在Rt△BDC中，BC=2，CD=1，根据勾股定理求得BD=，即可求得DE=.

∵△ABC为等边三角形，

∴∠ABC=∠ACB=60°，AC=BC，

∵BD为中线，

∴∠DBC=∠ABC=30°，∠BDC=90°，AD=CD=AC，

∵CD=CE=1，

∴∠E=∠CDE，AC=BC=2,

∵∠E+∠CDE=∠ACB=60°，

∴∠E=30°=∠DBC，

∴BD=DE，

在Rt△BDC中，BC=2，CD=1，

根据勾股定理求得BD=，

∴DE=BD=.