题目内容
如图,∠C=90º,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.
【小题1】用含有x的代数式表示CE的长
【小题2】求点F与点B重合时x的值
【小题3】当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式
【小题1】由题意知,△DBP∽△ABC,四边形PDEC为矩形,
∴ ,CE=PD.
,CE=PD.
∴ .∴
.∴ .
.
【小题2】由题意知,△CEF∽△CBA,∴ .∴
.∴ .
.
当点F与点B重合时, ,9x=20.解得
,9x=20.解得 .
.
【小题3】当点F与点P重合时, ,4x+9x=20.解得
,4x+9x=20.解得 .
.
当 时,如图①,
时,如图①,

 ............ (8分)
............ (8分)
当 ≤x<
≤x< 时,如图②,
时,如图②,

=
.
(或 ) (7分)
) (7分)
.......... (10分)
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的值为( ▲ )
的值为( ▲ )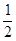 B.1 C.
B.1 C.

 △
△ 中,∠
中,∠ =90°,
=90°, =4,
=4, =5,点
=5,点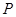 是
是 、点
、点 重合),PQ⊥
重合),PQ⊥ 的值为( ▲ )
的值为( ▲ )





 (B)
(B) (D)
(D) -3
-3