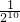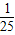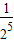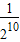题目内容

等边△ABC的各边与它的内切圆相切于A₁，B₁，C₁，△A₁B₁C₁的各边与它的内切圆相切于A₂，B₂，C₂，…，以此类推．若△ABC的面积为1，则△A₅B₅C₅的面积为（　　）

A．

1

5

B．

1

25

C．

1

25

D．

1

210

∵等边△ABC的各边与它的内切圆相切于A₁，B₁，C₁，设等边△ABC的内心为O，
∴点O也是等边△ABC的外心，
∴A₁，B₁，C₁分别是△ABC各边的中点，
设等边△ABC的边长为a，则根据三角形中位线定理，得出△A₁B₁C₁的边长为

1

2

a，
同理，等边△A₂B₂C₂的边长为（

1

2

）²a，
…，
等边△A₅B₅C₅的边长为（

1

2

）⁵a．
又∵△ABC∽△A₅B₅C₅，△ABC的面积为1，
∴△ABC的面积：△A₅B₅C₅的面积=[a：（

1

2

）⁵a]²，
∴△A₅B₅C₅的面积=

1

210

．
故选D．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

等边△ABC的各边与它的内切圆相切于A₁，B₁，C₁，△A₁B₁C₁的各边与它的内切圆相切于A₂，B₂，C₂，…，以此类推．若△ABC的面积为1，则△A₅B₅C₅的面积为（　　）

已知等边△ABC边长为a，D、E分别为AB、AC边上的动点，且在运动时保持DE∥BC，如图（1），⊙O₁与⊙O₂都不在△ABC的外部，且⊙O₁、⊙O₂分别与∠B和∠C的两边及DE都相切，其中和DE、BC的切点分别为M、N、M′、N′．
（1）求证：⊙O₁和⊙O₂是等圆；
（2）设⊙O₁的半径长为x，圆心距O₁O₂为y，求y与x的函数关系式，并写出x的取值范围；
（3）当⊙O₁与⊙O₂外切时，求x的值；
（4）如图（2），当D、E分别是AB、AC边的中点时，将⊙O₂先向左平移至和⊙O₁重合，然后将重合后的圆沿着△ABC内各边按图（2）中箭头的方向进行滚动，且总是与△ABC的边相切，当点O₁第一次回到它原来的位置时，求点O₁经过的路线长度？

等边△ABC的各边与它的内切圆相切于A₁，B₁，C₁，△A₁B₁C₁的各边与它的内切圆相切于A₂，B₂，C₂，…，以此类推．若△ABC的面积为1，则△A₅B₅C₅的面积为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

等边△ABC的各边与它的内切圆相切于A₁，B₁，C₁，△A₁B₁C₁的各边与它的内切圆相切于A₂，B₂，C₂，…，以此类推．若△ABC的面积为1，则△A₅B₅C₅的面积为（）
A．