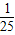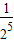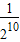题目内容
等边△ABC的各边与它的内切圆相切于A1,B1,C1,△A1B1C1的各边与它的内切圆相切于A2,B2,C2,…,以此类推.若△ABC的面积为1,则△A5B5C5的面积为
- A.

- B.

- C.

- D.
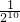
D
分析:设等边△ABC的边长为a,则可得出△A1B1C1是等边三角形,且边长为 a,同理,得出等边△A2B2C2的边长为(
a,同理,得出等边△A2B2C2的边长为( )2a,…,等边△A5B5C5的边长为(
)2a,…,等边△A5B5C5的边长为( )5a,由于所有的等边三角形都相似,所以根据相似三角形的面积比等于相似比的平方求出△A5B5C5的面积.
)5a,由于所有的等边三角形都相似,所以根据相似三角形的面积比等于相似比的平方求出△A5B5C5的面积.
解答:∵等边△ABC的各边与它的内切圆相切于A1,B1,C1,设等边△ABC的内心为O,
∴点O也是等边△ABC的外心,
∴A1,B1,C1分别是△ABC各边的中点,
设等边△ABC的边长为a,则根据三角形中位线定理,得出△A1B1C1的边长为 a,
a,
同理,等边△A2B2C2的边长为( )2a,
)2a,
…,
等边△A5B5C5的边长为( )5a.
)5a.
又∵△ABC∽△A5B5C5,△ABC的面积为1,
∴△ABC的面积:△A5B5C5的面积=[a:( )5a]2,
)5a]2,
∴△A5B5C5的面积=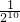 .
.
故选D.
点评:此题综合运用了等边三角形的性质、三角形的中位线定理、相似三角形的判定及性质,综合性较强,难度中等.
分析:设等边△ABC的边长为a,则可得出△A1B1C1是等边三角形,且边长为
 a,同理,得出等边△A2B2C2的边长为(
a,同理,得出等边△A2B2C2的边长为( )2a,…,等边△A5B5C5的边长为(
)2a,…,等边△A5B5C5的边长为( )5a,由于所有的等边三角形都相似,所以根据相似三角形的面积比等于相似比的平方求出△A5B5C5的面积.
)5a,由于所有的等边三角形都相似,所以根据相似三角形的面积比等于相似比的平方求出△A5B5C5的面积.解答:∵等边△ABC的各边与它的内切圆相切于A1,B1,C1,设等边△ABC的内心为O,
∴点O也是等边△ABC的外心,
∴A1,B1,C1分别是△ABC各边的中点,
设等边△ABC的边长为a,则根据三角形中位线定理,得出△A1B1C1的边长为
 a,
a,同理,等边△A2B2C2的边长为(
 )2a,
)2a,…,
等边△A5B5C5的边长为(
 )5a.
)5a.又∵△ABC∽△A5B5C5,△ABC的面积为1,
∴△ABC的面积:△A5B5C5的面积=[a:(
 )5a]2,
)5a]2,∴△A5B5C5的面积=
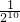 .
.故选D.
点评:此题综合运用了等边三角形的性质、三角形的中位线定理、相似三角形的判定及性质,综合性较强,难度中等.

练习册系列答案
相关题目