题目内容
6. 如图,已知矩形ABCD的边长AB=4,BC=6,对角线AC的垂直平分线分别交AC、AD、BC于O、E、F,连结AF、CE,则$\frac{AE}{BF}$=$\frac{13}{5}$.
如图,已知矩形ABCD的边长AB=4,BC=6,对角线AC的垂直平分线分别交AC、AD、BC于O、E、F,连结AF、CE,则$\frac{AE}{BF}$=$\frac{13}{5}$.
分析 由ASA证明△AOE≌△COF,得出对应边相等EO=FO,证出四边形AFCE为平行四边形,再由FE⊥AC,得出四边形AFCE为菱形,由菱形的性质得出AE=CF,AE=CE,得出DE=BF,设AE=CE=x.则DE=AD-x,CD=AB=4,由勾股定理得出方程,解方程求出AE,得出DE,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴AE∥FC,AD=BC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
在△AOE和△COF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}&{\;}\\{AO=CO}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AFCE为菱形.
∴AE=CF,AE=CE,
∴DE=BF,
设AE=CE=x.
则DE=AD-x,CD=AB=4.
根据勾股定理可得:x2=(6-x)2+42
解得:AE=$\frac{13}{3}$.
∴DE=6-$\frac{13}{3}$=$\frac{5}{3}$,
∴BF=$\frac{5}{3}$,
∴$\frac{AE}{BF}$=$\frac{13}{5}$;
故答案为$\frac{13}{5}$.
点评 本题考查了矩形的性质、菱形的判定方法、平行四边形的判定方法、全等三角形的判定与性质;熟练掌握矩形的性质,证明四边形是菱形是解决问题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
16.-3$\frac{1}{2}$的绝对值是( )
| A. | 3$\frac{1}{2}$ | B. | $-\frac{2}{7}$ | C. | $\frac{2}{7}$ | D. | $-\frac{2}{7}$ |
14.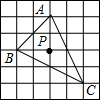 △ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )
△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )
 △ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )
△ABC在正方形网格中的位置如图所示,点A,B,C,P均在格点上,则点P是△ABC的( )| A. | 三条垂直平分线的交点 | B. | 三条内角角平分线的交点 | ||
| C. | 重心 | D. | 无法确定 |
1.$\sqrt{8}$-$\sqrt{2}$等于( )
| A. | $\sqrt{6}$ | B. | $3\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
18.方程1-3x=0的解是( )
| A. | x=-$\frac{1}{3}$ | B. | x=$\frac{1}{3}$ | C. | x=-3 | D. | x=3 |
16.下列各数中互为相反数的有( )
| A. | +(-5.2)与-5.2 | B. | +(+5.2)与-5.2 | C. | -(-5.2)与5.2 | D. | 5.2与+|-5.2| |
 如图所示的几何体是由以下四个图形中的哪一个图形绕着虚线旋转一周得到的( )
如图所示的几何体是由以下四个图形中的哪一个图形绕着虚线旋转一周得到的( )



 三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是25.
三国时期吴国赵爽创制了“勾股圆方图”(如图)证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的短的直角边长是3,则大正方形ABCD的面积是25. 如图,|a-b|-$\sqrt{{b}^{2}}$=a.
如图,|a-b|-$\sqrt{{b}^{2}}$=a.