题目内容
某公司汽车司机驾驶汽车运输货物从甲地运往乙地,他以60km/h的平均速度,用8小时把货物送达目的地.
(1)当他按原路返回时,汽车的平均速度v与时间t满足怎样的函数关系?
(2)如果公司要求该司机在送完货物后必须在6h内返回公司,则返程时的平均速度不能低于多少?
(1)当他按原路返回时,汽车的平均速度v与时间t满足怎样的函数关系?
(2)如果公司要求该司机在送完货物后必须在6h内返回公司,则返程时的平均速度不能低于多少?
考点:反比例函数的应用
专题:
分析:(1)先根据速度×时间=路程,求出甲地与乙地的路程;再根据行驶速度=路程÷时间,即可得到v与t的函数解析式;
(2)由(1)中的解析式和t≤6可得v的范围.
(2)由(1)中的解析式和t≤6可得v的范围.
解答:解:(1)由已知得:vt=60×8,
v=
;
(2)∵v=
,
∴t=
,
∵t≤6,
∴
≤6,
∴v≥80.
答:返程时的平均速度不能低于每小时80千米.
v=
| 480 |
| t |
(2)∵v=
| 480 |
| t |
∴t=
| 480 |
| v |
∵t≤6,
∴
| 480 |
| v |
∴v≥80.
答:返程时的平均速度不能低于每小时80千米.
点评:本题考查了反比例函数的应用,掌握路程、速度、时间三者之间的关系是解答本题的关键.

练习册系列答案
相关题目
已知⊙O的半径为2,圆心O到直线l的距离PO=1,则直线l与⊙O的位置关系是( )
| A、相切 | B、相离 |
| C、相交 | D、无法判断 |
 如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )
如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )| A、1个 | B、2个 | C、3个 | D、4个 |
下列命题中,正确的是( )
| A、全等三角形的高相等 |
| B、全等三角形的中线相等 |
| C、全等三角形的角平分线相等 |
| D、全等三角形对应边上的高相等 |
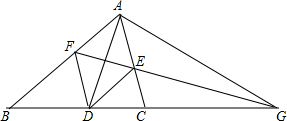 如图,AD是∠BAC的平分线,DE平行AB交AC于点E,DF平行AC交AB于点F,延长FE交BC的延长线于点G,求证:
如图,AD是∠BAC的平分线,DE平行AB交AC于点E,DF平行AC交AB于点F,延长FE交BC的延长线于点G,求证: 如图,AB为⊙O的直径,AD是⊙O的弦,E是AD的中点,连接OE并延长交⊙O于点C,若∠BAD=20°,求∠ACO的度数.
如图,AB为⊙O的直径,AD是⊙O的弦,E是AD的中点,连接OE并延长交⊙O于点C,若∠BAD=20°,求∠ACO的度数.