题目内容
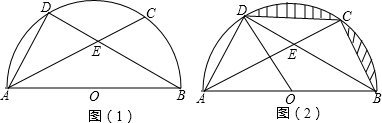 (2012•遂宁)已知:如图,AB是⊙O的直径,D是弧AC的中点,弦AC与BD相交于点E,AD=2
(2012•遂宁)已知:如图,AB是⊙O的直径,D是弧AC的中点,弦AC与BD相交于点E,AD=2| 3 |
(1)求直径AB的长;
(2)在图2中,连接DO,DC,BC.求证:四边形BCDO是菱形;
(3)求图2中阴影部分的面积.
分析:(1)证△ADE∽△BDA,推出
=
,求出BD,根据勾股定理求出AB即可;
(2)求出AB=2AD,求出AB=2BC,推出OB=OD=BC=CD,根据菱形的判定推出即可;
(3)求出∠DOB,求出菱形BCDO和扇形DOB的面积,即可求出答案.
| AD |
| BD |
| DE |
| AD |
(2)求出AB=2AD,求出AB=2BC,推出OB=OD=BC=CD,根据菱形的判定推出即可;
(3)求出∠DOB,求出菱形BCDO和扇形DOB的面积,即可求出答案.
解答:解:(1)∵D是弧AC的中点,
∴∠DAC=∠B,
∵∠ADE=∠BDA,
∴△ADE∽△BDA,
∴
=
,
∴BD=
=
=6,
∵AB是⊙O的直径,
∴∠ADB=90°.
在Rt△ABD中,由勾股定理,得AB=
=
=4
.
(2)∵在Rt△ABD中,AB=4
,AD=2
,
∴AB=2AD,
∴∠ABD=30°,∠DAB=60°,
∴∠ABD=∠DAC=∠CAB=30°,
∴CD=BC,
∵在Rt△ABC中,∠CAB=30°,
∴AB=2BC,
∴OB=OD=BC=CD,
∴四边形BCDO是菱形.
(3)连接OC,
∵OD=OB,∠DBA=30°,
∴∠ODB=∠OBD=30°,
∴∠DOB=120°,
∵四边形BCDO是菱形,
∴BD⊥OC,
∴菱形BCDO的面积是S=
BD×OC=
×6×2
=6
,
∵扇形BCD的面积是S′=
=4π,
∴S阴影=S′-S=4π-6
.
∴∠DAC=∠B,
∵∠ADE=∠BDA,
∴△ADE∽△BDA,
∴
| AD |
| BD |
| DE |
| AD |
∴BD=
| AD2 |
| DE |
(2
| ||
| 2 |
∵AB是⊙O的直径,
∴∠ADB=90°.
在Rt△ABD中,由勾股定理,得AB=
| BD2+AD2 |
| 36+12 |
| 3 |
(2)∵在Rt△ABD中,AB=4
| 3 |
| 3 |
∴AB=2AD,
∴∠ABD=30°,∠DAB=60°,
∴∠ABD=∠DAC=∠CAB=30°,
∴CD=BC,
∵在Rt△ABC中,∠CAB=30°,
∴AB=2BC,
∴OB=OD=BC=CD,
∴四边形BCDO是菱形.
(3)连接OC,

∵OD=OB,∠DBA=30°,
∴∠ODB=∠OBD=30°,
∴∠DOB=120°,
∵四边形BCDO是菱形,
∴BD⊥OC,
∴菱形BCDO的面积是S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵扇形BCD的面积是S′=
120×π×(2
| ||
| 360 |
∴S阴影=S′-S=4π-6
| 3 |
点评:本题综合考查了相似三角形的性质和判定,扇形的面积,菱形的性质和判定,含30度角的直角三角形的性质,圆心角、弧、弦之间的关系,勾股定理,圆周角定理等知识点的应用,有一定的难度.

练习册系列答案
相关题目
 (2012•遂宁)已知:如图,直线y=mx+n与抛物线
(2012•遂宁)已知:如图,直线y=mx+n与抛物线 (2012•遂宁)已知:如图,△ABC中,AB=AC,AD⊥BC垂足为D.将△ADC绕点D逆时针旋转90°后,点A落在BD上点A1处,点C落在DA延长线上点C1处,A1C1与AB交于点E.
(2012•遂宁)已知:如图,△ABC中,AB=AC,AD⊥BC垂足为D.将△ADC绕点D逆时针旋转90°后,点A落在BD上点A1处,点C落在DA延长线上点C1处,A1C1与AB交于点E.