题目内容
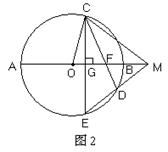
.(12分)如图1:⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在 上取一点D,分别作直线CD、ED交直线AB于点F、M。
上取一点D,分别作直线CD、ED交直线AB于点F、M。
(1)求∠COA和∠FDM的度数;(3分)
(2)求证:△FDM∽△COM;(4分)
(3)如图2:若将垂足G改取为半径OB上任意一点,点D改取在 上,仍作直线CD、ED,分别交直线AB于点F、M,试判断:此时是否仍有△FDM∽△COM?证明你的结论。(5分)
上,仍作直线CD、ED,分别交直线AB于点F、M,试判断:此时是否仍有△FDM∽△COM?证明你的结论。(5分)
(1)∵AB为直径,CE⊥AB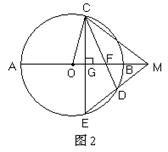
∴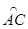 =
=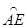 ,CG=EG
,CG=EG
在Rt△COG中,
∵OG=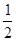 OC
OC
∴∠OCG=300,∠COA=600
又∵∠CDE的度数
=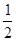 弧CAE的度数
弧CAE的度数
=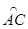 的度数
的度数
=∠COA的度数=600
∴∠FDM=1800-∠CDE=1200
(2)证明:
∵∠COM=1800-∠COA=1200
∴∠COM=∠FDM
在Rt△CGM和Rt△EGM中
∵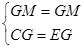 ∴Rt△CGM≌Rt△EGM ∴∠GMC=∠GME
∴Rt△CGM≌Rt△EGM ∴∠GMC=∠GME
又∠DMF=∠GME ∴∠OMC=∠DMF ∴△FDM∽△COM
(3)解:结论仍成立。
∵∠FDM=1800-∠CDE
∴∠CDE的度数=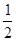 弧CAE的度数=
弧CAE的度数=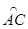 的度数=∠COA的度数
的度数=∠COA的度数
∴∠FDM=1800-∠COA=∠COM
∵AB为直径,CE⊥AB; ∴在Rt△CGM和Rt△EGM中
∵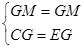
∴Rt△CGM≌Rt△EGM
∴∠GMC=∠GME
∴△FDM∽△COM
解析

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 ,求此时直线PM的解析式;
,求此时直线PM的解析式;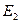 ,PM的延长线与CD的延长线交于点F,若三角形G
,PM的延长线与CD的延长线交于点F,若三角形G
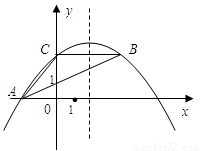
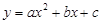 的图象与x轴交于两个不同的点A(-2,0)、B(4,0),与y轴交于点C(0,3),连结BC、AC,该二次函数图象的对称轴与x轴相交于点D.
的图象与x轴交于两个不同的点A(-2,0)、B(4,0),与y轴交于点C(0,3),连结BC、AC,该二次函数图象的对称轴与x轴相交于点D.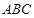 相似,求出点Q的坐标;
相似,求出点Q的坐标;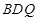 外接圆圆心的坐标.
外接圆圆心的坐标.
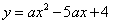 经过
经过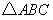 的三个顶点,已知
的三个顶点,已知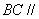
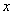 轴,点
轴,点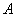 在
在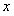 轴上,点
轴上,点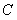 在
在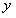 轴上,且
轴上,且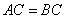 .
.
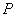 是抛物线对称轴上且在
是抛物线对称轴上且在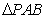 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点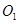 和⊙
和⊙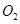 相交于A、B两点,⊙
相交于A、B两点,⊙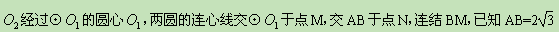
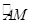 的长。
的长。