题目内容
 如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为
如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为
- A.

- B.

- C.

- D.

A
分析:如图:根据矩形的性质,∠BOC=60°,AD=3可得OD=OA=AD,再根据直角三角形的性质,可得OF、OE、CG的长,S△POC要分类讨论,当0≤x<3时,y=S△POC=S△ACD-S△APO-S△PDC,可得y与x的函数关系,当3<x≤6时,y=S△POC,可得y与x的函数关系.
解答: 解:作OE⊥DC,作OF⊥AD,作CG⊥DB,
解:作OE⊥DC,作OF⊥AD,作CG⊥DB,
∵矩形ABCD,AD=3,
∴BC=3,
∵矩形ABCD的对角线交于点O,∠BOC=60°,
∴△BOC是等边三角形,OB=OC=BC=3,
∵△BOC≌△AOD,
∴∠ADO=∠AOD=60°,DO=AO=3,
在Rt△OAF中,∠AOF=30°,OA=3,AF= ,
,
∴由勾股定理得OF=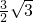 ,
,
在Rt△DOE中,∠ODE=30°,OD=3,
∴OE= ,
,
由勾股定理得DE=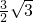 ,
,
∴DC=2DE=3 ,
,
在Rt△DCG中,∠CDG=30°,DC=3 ,
,
∴CG=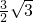 ,
,
当0≤x<3时,y=S△POC=S△ACD-S△APO-S△PDC
= ×3×
×3× -
- ×
×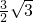 •x-
•x- ×(3-x)
×(3-x)
= x,
x,
即y是x的正比例函数,
当3<x≤6时,y=S△POC= (x-3)•
(x-3)• ,
,
即y是x的一次函数,
故选:A.
点评:本题考查了分段函数图象,根据矩形的性质、直角三角形的性质求出相关边的长是解题关键,对y=S△POC的表示要分类.
分析:如图:根据矩形的性质,∠BOC=60°,AD=3可得OD=OA=AD,再根据直角三角形的性质,可得OF、OE、CG的长,S△POC要分类讨论,当0≤x<3时,y=S△POC=S△ACD-S△APO-S△PDC,可得y与x的函数关系,当3<x≤6时,y=S△POC,可得y与x的函数关系.
解答:
 解:作OE⊥DC,作OF⊥AD,作CG⊥DB,
解:作OE⊥DC,作OF⊥AD,作CG⊥DB,∵矩形ABCD,AD=3,
∴BC=3,
∵矩形ABCD的对角线交于点O,∠BOC=60°,
∴△BOC是等边三角形,OB=OC=BC=3,
∵△BOC≌△AOD,
∴∠ADO=∠AOD=60°,DO=AO=3,
在Rt△OAF中,∠AOF=30°,OA=3,AF=
 ,
,∴由勾股定理得OF=
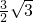 ,
,在Rt△DOE中,∠ODE=30°,OD=3,
∴OE=
 ,
,由勾股定理得DE=
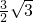 ,
,∴DC=2DE=3
 ,
,在Rt△DCG中,∠CDG=30°,DC=3
 ,
,∴CG=
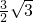 ,
,当0≤x<3时,y=S△POC=S△ACD-S△APO-S△PDC
=
 ×3×
×3× -
- ×
×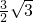 •x-
•x- ×(3-x)
×(3-x)
=
 x,
x,即y是x的正比例函数,
当3<x≤6时,y=S△POC=
 (x-3)•
(x-3)• ,
,即y是x的一次函数,
故选:A.
点评:本题考查了分段函数图象,根据矩形的性质、直角三角形的性质求出相关边的长是解题关键,对y=S△POC的表示要分类.

练习册系列答案
相关题目
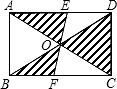 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为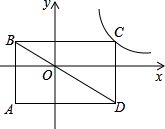 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y= 如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线 (2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )
(2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( ) 如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=
如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=