题目内容
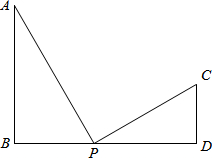
如图，已知AB⊥BD，AC⊥CD，∠A=35°，则∠D的度数为
- A.35°
- B.65°
- C.55°
- D.45°
A
分析：由三角形的一个外角等于与它不相邻的两个内角的和，得∠CEB=∠A+∠B=35°+90°=125°，同理∠CEB=∠C+∠D，代入即可求解．
解答：∵AB⊥BD，∠A=35°，
∴∠CEB=∠A+∠B=35°+90°=125°，
同理∠CEB=∠C+∠D，
∴∠D=125-90°=35°．
故选A．
点评：用到的知识点为：三角形的一个外角等于与它不相邻的两个内角的和．
分析：由三角形的一个外角等于与它不相邻的两个内角的和，得∠CEB=∠A+∠B=35°+90°=125°，同理∠CEB=∠C+∠D，代入即可求解．
解答：∵AB⊥BD，∠A=35°，
∴∠CEB=∠A+∠B=35°+90°=125°，
同理∠CEB=∠C+∠D，
∴∠D=125-90°=35°．
故选A．
点评：用到的知识点为：三角形的一个外角等于与它不相邻的两个内角的和．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9、如图，已知AB⊥BD，ED⊥BD，C是BD上一点，AB=CD，BC=ED，那么下列结论中，不正确的是（ ）
49、如图，已知AB⊥BD，垂足为B，ED⊥BD，垂足为D，AB=CD，BC=DE，则∠ACE=
（2013•永州）如图，已知AB⊥BD，CD⊥BD
如图，已知AB⊥BD，BC⊥CD，AD=a，CD=b，则BD的长的取值范围为（ ）